Misurare

Come effettuare corrette misurazioni di parametri ambientali.

Metrologia

Scienza della misurazione e delle sue applicazioni

• Vocabolario internazionale di metrologia * https://www.ceinorme.it/it/normazione-it/vim/vim-content-it * Terminologia per le misurazioni analitiche Introduzione al VIM 3 pdf

• https://www.iso.org/obp/ui/

Monitoraggio ambientale

Il monitoraggio ambientale descrive i processi e le attività che devono aver luogo per caratterizzare e monitorare la qualità dell'ambiente.

Il monitoraggio ambientale viene utilizzato quando le attività umane comportano un rischio di effetti dannosi sull'ambiente naturale o viceversa. Serve per stabilire lo stato attuale di un ambiente o tendenze dei parametri ambientali.

I risultati del monitoraggio saranno rivisti, analizzati statisticamente e pubblicati. La progettazione di un programma di monitoraggio deve pertanto tenere conto dell'uso finale dei dati prima dell'inizio del monitoraggio.

• Aria

• Acqua

• Suolo

Componenti fisiche, chimiche, biologiche, radiologiche ...

Definizioni

Data Level

• Dati Level I , sono le letture dirette degli strumenti espresse in appropriate unità fisiche e georeferenziate

• Dati Level II, dati riconosciuti come variabili meteorologiche; possono essere ottenuti direttamente da strumenti o derivati dai dati Level I

• Dati Level III sono quelli contenuti in dataset internamente consistenti, generalmente su grigliato.

I dati scambiati a livello internazionale sono livello II o livello III

Campionamento

Processo per ottenere una sequenza discreta di misurazioni di una grandezza.

Campione

Una singola misura, in genere una di una serie di letture spot di un sistema di sensori. Si noti che questo differisce dal significato usuale in statistica di un insieme di numeri o misure che fa parte di una popolazione.

Un'osservazione

Il risultato del processo di campionamento, ovvero la quantità riportata o registrata (spesso chiamata anche misura). Nel contesto dell'analisi delle serie temporali, un'osservazione deriva da un certo numero di campioni.

Una misura

La definizione ISO è "un insieme di operazioni aventi per oggetto la determinazione del valore di una grandezza". Nell'uso comune, il termine può essere utilizzato per indicare il valore di un campione o di un'osservazione.

Tempo di campionamento o periodo di osservazione

La durata del tempo in cui viene effettuata un'osservazione, durante la quale vengono prelevati un certo numero di campioni individuali.

Intervallo di campionamento

L'intervallo di tempo tra osservazioni successive.

Funzione di campionamento o funzione di ponderazione

Nella sua definizione più semplice, un algoritmo per calcolare la media o filtrare i singoli campioni.

Frequenza di campionamento

La frequenza con cui vengono prelevati i campioni. La distanza tra i campioni è il tempo che intercorre tra un campione e l'altro.

Attenuazione

Processo di attenuazione delle componenti ad alta frequenza dello spettro senza influenzare in modo significativo le frequenze più basse. Di solito viene effettuato per rimuovere il rumore (errori e fluttuazioni casuali non rilevanti per l'applicazione).

Filtro

Dispositivo che consente di attenuare o selezionare le frequenze prescelte. L'attenuazione viene eseguita da un filtro passa-basso e i termini attenuazione e filtraggio sono spesso usati in modo intercambiabile in questo senso. In questo senso. Tuttavia, esistono anche filtri passa-alto e passa-banda. Il filtraggio può essere una proprietà dello strumento, come l'inerzia, oppure può essere eseguito elettronicamente o numericamente.

Accuratezza e Precisione

L’accuratezza è la vicinanza di un valore misurato al suo valore reale (accuracy is the closeness of a measured value to its true value) e in buona parte dipende dallo strumento. Per esempio, nelle misure ecologiche, il metodo delle trappole per la stima della quantità di individui in una popolazione e quello del C-14 per la produzione di plancton nell’oceano tropicale hanno una accuratezza molto bassa; cioè possono essere molto distanti dal valore reale. Ogni stima, ripetuta nelle stesse condizioni, può dare la metà del valore reale. Uno strumento o un reagente che forniscono una risposta sbagliata spesso sono tarati in modo non corretto e sono definiti inaccurati; i valori ottenuti sono biased.

Nel processo di misurazione con uno strumento inaccurato si commette un errore sistematico, chiamato appunto bias. Esso rappresenta un problema importante e ricorrente, in molte tecniche di stima di una quantità. In varie discipline, il progresso è spesso collegato alla ricerca di metodi di misurazione più accurati.

La precisione (ripetibilità) è la vicinanza di misure ripetute al medesimo valore (precision is the closeness of repeated measuments to the same item). Spesso dipende dalla capacità del tecnico di ripetere la misurazione con le stesse modalità e ha origine dalla sua esperienza o abilità.

I concetti di accuracy, precision e bias applicati a una misura di peso sono rappresentati graficamente nella figura successiva tratta dall’ottimo testo, per la stima di popolazioni animali e vegetali, di Charles J. Krebs del 1999 (Ecological methodology, 2nd ed. Menlo Park, CA, Cummings, pp. XII, 620),

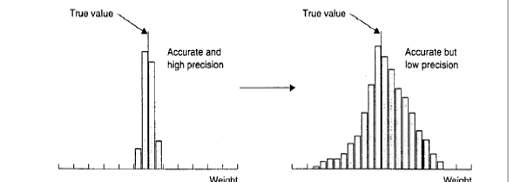
figura A e B

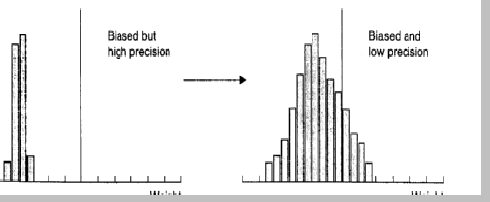
figura C e D

• Nella figura A le misure sono accurate, vicine al valore vero (true value), e molto precise (high precision).

• Nella figura B le misure sono accurate ma poco precise (low precision), cioè differenti tra loro.

• Nella figura C le misure sono non accurate (biased) ma molto precise (high precision).

• Nella figura D le misure sono non accurate (biased) e poco precise (low precision).

Esempio: la differenza tra accuratezza e precisione si può spiegare facilmente utilizzando l’analogia di una freccia lanciata verso un bersaglio. L’accuratezza descrive la vicinanza della freccia al barilotto.

tiro accurato

tiro preciso

Se venissero lanciate diverse frecce, la precisione verrebbe indicata dalle dimensioni del gruppo di frecce. Se le frecce sono raggruppate tutte insieme, il tiro viene considerato preciso.

Leggi di scala

Le leggi di scala riguardano il comportamento di una struttura in funzione della scala da cui la si guarda. Per i sistemi regolari, sia matematici sia fisici e naturali, il sistema a grande scala è, in genere, molto diverso da quello a piccola scala. Per esempio, la Terra è un punto rispetto alla scala galattica, poi se ci si avvicina appare come una sfera, dopo ancora come una superficie quasi piana, in seguito appaiono i rilievi montuosi e le coste, poi le città, e così via. Le strutture matematiche usuali sono, in genere, molto più semplici e perdono struttura alle scale molto piccole. Per esempio, una sfera può essere approssimata dal suo piano tangente.

A partire dalla struttura stessa dell'Universo a grande scala, passando per le complesse forme delle strutture biologiche, fino alle interazioni elementari tra i costituenti fondamentali della materia, tutti questi sistemi mostrano delle ben definite leggi di scala. Queste leggi caratterizzano il cambiamento del sistema sotto l'effetto di una trasformazione della scala delle lunghezze, e rappresentano un elemento essenziale per la comprensione della complessità del sistema.

Per un sistema con una scala caratteristica, come un atomo, le leggi di scala non sono particolarmente interessanti. Infatti, se consideriamo una scala di lunghezze dell'ordine di quella dell'atomo stesso, potremo definire in modo adeguato tutte le sue proprietà: il nucleo centrale e la distribuzione degli elettroni intorno a esso. Se però consideriamo una scala molto più grande, l'atomo diventa a tutti gli effetti puntiforme e non mostra proprietà particolarmente interessanti. Questa situazione cambia completamente se prendiamo in esame una struttura molto familiare, ma abbastanza complessa, come quella di un albero. In questo caso possiamo partire dagli atomi che formano molecole, che poi formano le cellule, le fibre, quindi le più piccole foglie e i rami, i quali sono man mano più grandi e mostrano ramificazioni sia a piccole sia a grandi scale. Infine, arriviamo all'intero albero che, per scale molto più grandi, può essere considerato anch'esso puntiforme. Esiste però un'ampia varietà di scale in cui le proprietà sono abbastanza simili, per esempio la biforcazione dei rami avviene sia per i rami piccoli sia per quelli più grandi. In questa regione di scale, diciamo dalle fibre al tronco, possiamo definire un'approssimativa invarianza di scala con le sue proprietà caratteristiche. Questa proprietà naturalmente si estende da una scala minima, quella delle fibre, a una massima, quella del tronco o dell'albero stesso. Queste proprietà di scala sono essenziali per la comprensione delle complessità della struttura e della sua funzionalità, e costituiscono una delle caratterizzazioni fondamentali delle strutture complesse.

Data level nelle RMAP RFC

Campionamento delle variabili

Le variabili atmosferiche come la velocità del vento, la temperatura, la pressione e l'umidità sono funzioni di quattro dimensioni: due orizzontali, una verticale e una temporale. Esse variano irregolarmente in tutte e quattro e lo scopo dello studio del campionamento è quello di definire procedure di misurazione pratiche per ottenere osservazioni rappresentative con incertezze accettabili nelle stime della media e della variabilità.

L'argomento può essere affrontato a due livelli:

1. A livello elementare, si può discutere il problema meteorologico di base, che consiste nell'ottenere un valore medio di una grandezza fluttuante rappresentativa di un determinato intervallo di campionamento in un dato momento, utilizzando sistemi strumentali con tempi di risposta lunghi rispetto alle fluttuazioni. Al livello più semplice, ciò comporta considerazioni sulle statistiche di un insieme di misure e dei tempi di risposta degli strumenti e dei circuiti elettronici;

2. Il problema può essere considerato in modo più preciso facendo uso della teoria dell'analisi delle serie temporali, del concetto di spettro delle fluttuazioni e del comportamento dei filtri. Questi argomenti sono necessari per il problema più complesso dell'utilizzo di strumenti a risposta relativamente rapida per ottenere misure soddisfacenti della media o dello spettro di una grandezza che varia rapidamente, come il vento.

È importante riconoscere che una variabile atmosferica in realtà non viene mai campionata. È solo possibile avvicinarsi il più possibile campionando l'uscita di un sensore di quella variabile. La distinzione è importante perché i sensori non creano un analogo esatto della variabile rilevata. In generale, i sensori rispondono più lentamente dei cambiamenti dell'atmosfera e aggiungono rumore.

I sensori fanno anche altre cose, di solito indesiderabili, come la deriva nella calibrazione, la risposta non lineare, l'interferenza con la grandezza che stanno misurando, il fallimento più frequente di quanto previsto e così via, ma questa discussione riguarderà solo la risposta e l'aggiunta di rumore.

Rappresentatività nel tempo e nello spazio

Le osservazioni campionarie vengono effettuate a una frequenza e per un intervallo di tempo limitati su un'area circoscritta. In pratica, le osservazioni dovrebbero essere progettate in modo da essere sufficientemente frequenti da essere rappresentative delle parti non campionate della variabile (continua) e sono spesso considerate rappresentative di un intervallo di tempo più lungo e di un'area più ampia.

L'utente di un'osservazione si aspetta che sia rappresentativa, o tipica, di un'area e di un tempo, e di un intervallo di tempo. Quest'area, ad esempio, può essere "l'aeroporto" o l'area compresa in un raggio di diversi chilometri e facilmente visibile da un osservatore umano. L'ora è quella in cui è stata fatta la segnalazione o è stato trasmesso il messaggio, mentre l'intervallo è una quantità concordata, spesso 1, 2 o 10 minuti.

Per rendere rappresentative le osservazioni, i sensori vengono esposti ad altezze standard e in posizioni non ostruite e i campioni vengono elaborati per ottenere valori medi. In alcuni casi, i sensori, ad esempio i trasmissometri, hanno una media spaziale intrinseca, che contribuisce alla rappresentatività dell'osservazione. L'osservazione umana della visibilità ne è un altro esempio. Tuttavia, il resto della discussione in questo capitolo ignorerà il campionamento spaziale e si concentrerà sul campionamento temporale delle misure effettuate in un punto.

Un esempio tipico di campionamento e media temporale è la misurazione della temperatura ogni minuto (i campioni), il calcolo di una media di 10 minuti (l'intervallo di campionamento e la funzione di campionamento) e la trasmissione di questa media (l'osservazione) in un rapporto sinottico ogni 3 ore.

Quando queste osservazioni vengono raccolte per un periodo dallo stesso sito, diventano esse stesse campioni in una nuova sequenza temporale con uno spazio di 3 ore. Quando vengono raccolte da un gran numero di siti, anche queste osservazioni diventano campioni in una sequenza spaziale. In questo senso, le osservazioni rappresentative sono anche campioni rappresentativi. In questo capitolo discutiamo dell'osservazione iniziale.

Gli spettri delle grandezze atmosferiche

Applicando l'operazione matematica nota come trasformata di Fourier, una funzione irregolare del tempo (o della distanza) può essere ridotta al suo spettro, che è la somma di un gran numero di sinusoidi, ciascuna con la propria ampiezza, lunghezza d'onda (o periodo o frequenza) e fase. In generale, queste lunghezze d'onda (o frequenze) definiscono "scale" o "scale di moto" dell'atmosfera.

La gamma di queste scale è limitata nell'atmosfera. A un estremo dello spettro, le scale orizzontali non possono superare la circonferenza della Terra o circa 40 000 km. Per scopi meteorologici, le scale verticali non superano le poche decine di chilometri. Nella dimensione temporale, invece, le scale più lunghe sono quelle climatologiche e, in linea di principio, non hanno limiti, ma in pratica il periodo più lungo non supera la lunghezza dei record. All'estremità breve, la dissipazione viscosa dell'energia turbolenta in calore stabilisce un limite inferiore. Vicino alla superficie della Terra, questo limite si trova a una lunghezza d'onda di pochi centimetri e aumenta con l'altezza fino a pochi metri nella stratosfera. Nella dimensione temporale, queste lunghezze d'onda corrispondono a frequenze di decine di hertz. È corretto dire che le variabili atmosferiche hanno una larghezza di banda limitata.

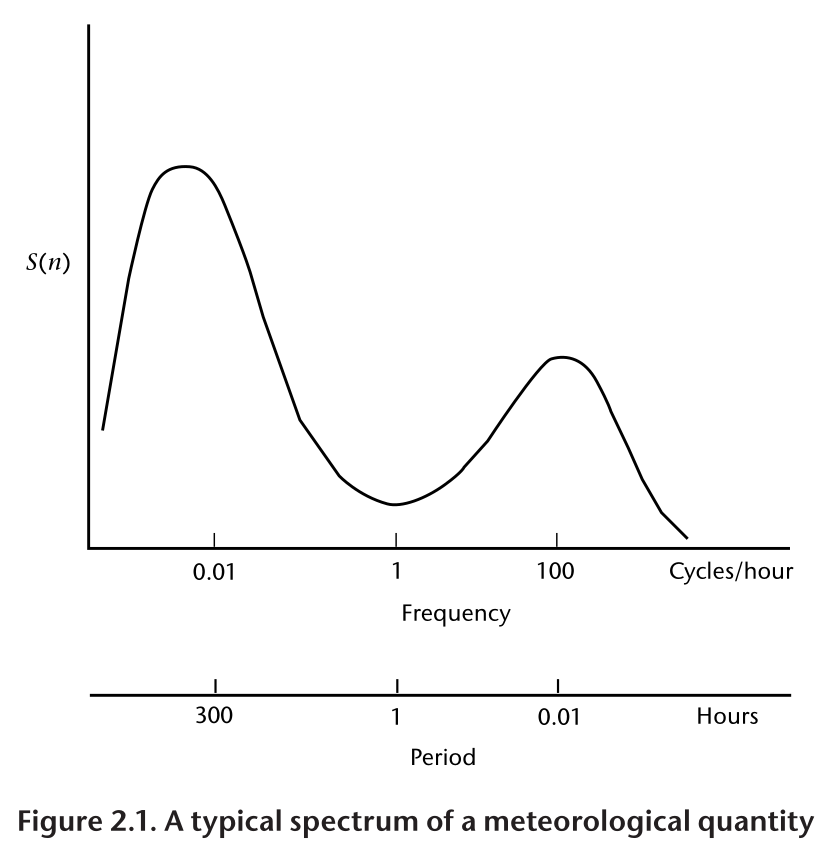
La Figura 2.1 è una rappresentazione schematica dello spettro di una grandezza meteorologica come il vento, misurato in una particolare stazione e in un determinato momento.

L'ordinata, comunemente chiamata energia o densità spettrale, è legata alla varianza delle fluttuazioni del vento ad ogni frequenza n. Lo spettro della Figura 2.1 ha un minimo di energia alla mesoscala intorno a un ciclo all'ora, tra picchi nella scala sinottica intorno a un ciclo ogni quattro giorni e nella microscala intorno a un ciclo al minuto. Le lunghezze d'onda più piccole sono di pochi centimetri e le frequenze più grandi sono di decine di hertz.

Serie temporali, spettri di potenza e filtri

Questa sezione è un'introduzione per i non addetti ai lavori ai concetti di analisi delle serie temporali che sono alla base delle buone pratiche di campionamento. Nel contesto della presente Guida, sono particolarmente importanti per la misurazione del vento, ma gli stessi problemi si presentano per la temperatura, la pressione e altre grandezze. Sono diventati importanti per le misurazioni meteorologiche di routine quando sono state introdotte le misurazioni automatiche, perché in tal modo è stato possibile effettuare campionamenti frequenti e veloci. Se i sistemi non sono progettati correttamente, possono verificarsi gravi errori nelle stime della media, degli estremi e dello spettro.

Sebbene le misure di spettro non siano di routine, hanno molte applicazioni. Lo spettro del vento è importante per l'ingegneria, la dispersione atmosferica, la diffusione e la dinamica. I concetti qui discussi sono utilizzati anche per l'analisi quantitativa dei dati satellitari (nella dimensione spaziale orizzontale) e in climatologia e micrometeorologia.

In sintesi, l'argomentazione è la seguente:

1. La frequenza di campionamento ottimale può essere valutata considerando la variabilità della grandezza da misurare. Le stime della media e di altre statistiche delle osservazioni avranno incertezze minori con frequenze di campionamento più elevate, cioè con campioni più grandi;

2. Il teorema di Nyquist afferma che una grandezza continua e fluttuante può essere determinata con precisione da una serie di campioni equispaziati se sono sufficientemente vicini;

3. Se la frequenza di campionamento è troppo bassa, le fluttuazioni alle frequenze più alte non campionate (al di sopra della frequenza di Nyquist) influenzeranno la stima del valore medio. Esse influenzeranno anche il calcolo delle frequenze più basse e lo spettro misurato non sarà corretto. Questo fenomeno è noto come aliasing. Può causare gravi errori se non viene compreso e tenuto in considerazione nella progettazione del sistema;

4. L'aliasing può essere evitato utilizzando una frequenza di campionamento elevata o filtrando in modo da poter utilizzare una frequenza di campionamento più bassa e conveniente;

5. I filtri possono essere digitali o analogici. Un sensore con un tempo di risposta adeguatamente lungo funge da filtro.

Una comprensione completa del campionamento implica la conoscenza degli spettri di potenza, del teorema di Nyquist, del filtraggio e della risposta degli strumenti. Si tratta di una materia altamente specializzata, che richiede la comprensione delle caratteristiche dei sensori utilizzati, del modo in cui l'uscita dei sensori viene condizionata, elaborata e registrata, delle proprietà fisiche degli elementi misurati e dello scopo per cui i dati analizzati devono essere utilizzati. A sua volta, ciò può richiedere competenze nella fisica degli strumenti, nella teoria dei sistemi elettronici o di altro tipo utilizzati nei processi di condizionamento e registrazione, nella matematica, nella statistica e nella meteorologia dei fenomeni, tutte cose che vanno ben oltre lo scopo di questo capitolo.

Tuttavia, è possibile per un non esperto comprendere i principi di buona pratica nella misurazione delle medie e degli estremi e apprezzare i problemi associati alle misure degli spettri.

Analisi delle serie temporali

È necessario considerare i segnali nel dominio del tempo o della frequenza. L'idea fondamentale fondamentale dell'analisi spettrale è il concetto di trasformata di Fourier. Una funzione, f(t), definita tra t = 0 e t = τ può essere trasformata nella somma di un insieme di funzioni sinusoidali:

\[f(t)=\sum_{j=0 }^{\infty}\alpha_{j}\sin(j\omega t + \phi_{j})\]

l'ampiezza e la fase associate a ciascun contributo spettrale sono α j e ϕ j . Entrambi possono essere influenzati dal campionamento e dall'elaborazione.

Finora si è ipotizzato che la funzione f(t) sia nota in modo continuo in tutto l'intervallo da t = 0 a t = τ. In realtà, nella maggior parte degli esempi questo non è il caso; la variabile meteorologica viene misurata in punti discreti di una serie temporale, che è una serie di N campioni equidistanti l'uno dall'altro Δt durante un periodo specifico τ = (N-1)Δt. Si presume che i campioni vengano prelevati istantaneamente, un'ipotesi che non è assolutamente vera, poiché tutti i dispositivi di misura richiedono un certo tempo per determinare il valore che stanno misurando. Nella maggior parte dei casi, questo tempo è breve rispetto alla distanza tra i campioni Δt.

Anche se non lo è, il tempo di risposta del sistema di misura può essere tenuto in considerazione nell'analisi, anche se non verrà trattato in questa sede.

Se si considerano i dati che si otterrebbero campionando una funzione sinusoidale a intervalli di tempo Δt, si può notare che la frequenza più alta che può essere rilevata è 1/(2Δt), e che in realtà qualsiasi sinusoide di frequenza più alta che possa essere presente nella serie temporale è rappresentata nei dati come se avesse una frequenza più bassa. La frequenza 1/(2Δt) è chiamata frequenza di Nyquist, qui indicata come \(n_{y}\) . La frequenza di Nyquist è talvolta chiamata frequenza di ripiegamento. Questa terminologia deriva dalla considerazione dell'aliasing dei dati. Il concetto è illustrato schematicamente nella Figura successiva.

Quando si effettua un'analisi spettrale di una serie temporale, a causa della natura discreta dei dati, il contributo alla stima alla frequenza n contiene anche contributi da frequenze più alte, cioè da 2 jn y ± n (j = 1 a ∞). Un modo per visualizzare questo aspetto è quello di considerare il dominio delle frequenze come se fosse piegato, in modo concertato, a n = 0 e n = \(n_{y}\) e così via a passi di \(n_{y}\).

La stima spettrale a ciascuna frequenza dell'intervallo è la somma di tutti i contributi delle frequenze superiori che la sovrastano.

Gli effetti pratici dell'aliasing sono illustrati al capitolo frequenza di campionamento. È un problema potenzialmente serio e deve essere preso in considerazione quando si progettano sistemi strumentali. Può essere evitato minimizzando, o riducendo a zero, l'intensità del segnale a frequenze superiori a \(n_{y}\). Ci sono un paio di modi per ottenere questo risultato. In primo luogo, il sistema può contenere un filtro passa-basso che attenua i contributi alle frequenze superiori a \(n_{y}\) prima che il segnale venga digitalizzato. L'unico svantaggio di questo approccio è che la tempistica e l'entità delle variazioni rapide non saranno registrate bene, o addirittura per niente.

Il secondo approccio consiste nell'avere un Δt abbastanza piccolo da rendere insignificanti i contributi al di sopra della frequenza di Nyquist. Questo è possibile perché gli spettri della maggior parte delle variabili meteorologiche cadono molto rapidamente a frequenze molto alte. Questo secondo approccio, tuttavia, non sarà sempre praticabile, come nell'esempio delle misure di temperatura su tre ore, dove se Δt è dell'ordine delle ore, le fluttuazioni su piccola scala non sono in grado di soddisfare le esigenze di un'analisi di temperatura dell'ordine delle ore, le fluttuazioni su piccola scala, dell'ordine dei minuti o dei secondi, possono avere ordinate spettrali relativamente grandi e alias forti. In questo caso, il primo metodo può essere appropriato.

Misurazione degli spettri

La densità spettrale, almeno così come viene stimata da una serie temporale, è definita come:

\[S(n_{j}) = (A_{j}^{2}+B_{j}^{2})/n_{y} = \alpha_{j}^{2}/n_{j}\]

Si noti che la fase non è rilevante in questo caso.

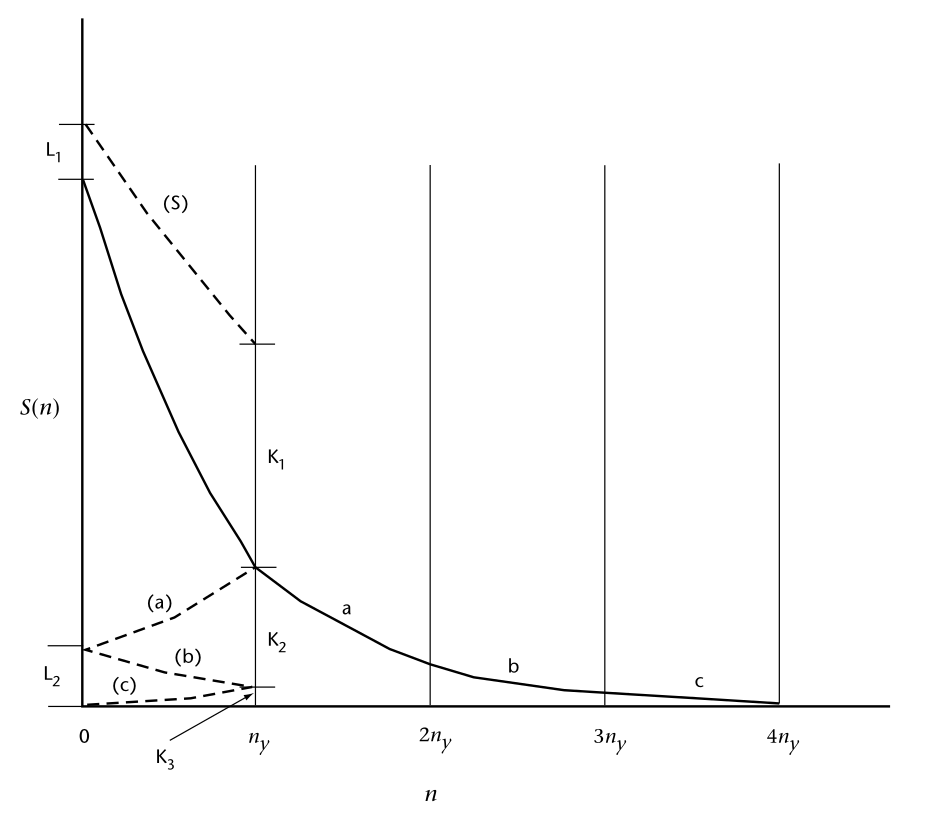
Illustrazione schematica dell'aliasing di uno spettro calcolato da una serie temporale stazionaria. Lo spettro può essere calcolato solo nell'intervallo di frequenza da zero alla frequenza di Nyquist \(n_{y}\). I valori reali delle energie alle frequenze più alte sono indicati dai settori contrassegnati con a, b e c. Questi sono "ripiegati" sul settore da n = 0 a \(n_{y}\), come indicato dalle linee spezzate (a), (b), (c). Lo spettro calcolato, indicato dalla linea spezzata in grassetto (S), include la somma di questi settori.

Lo spettro di una grandezza fluttuante può essere misurato in diversi modi. In passato, in elettrotecnica, veniva spesso determinato facendo passare il segnale attraverso filtri passa-banda e misurando la potenza in uscita. Questa veniva poi messa in relazione con la potenza della frequenza centrale del filtro.

Esistono diversi modi per affrontare l'analisi spettrale numerica di una serie temporale. Il più ovvio è la trasformata di Fourier diretta della serie temporale. In questo caso, poiché la serie ha una lunghezza finita, la trasformazione avrà solo un numero finito di componenti di frequenza.

Se ci sono N termini nella serie temporale, ci saranno N/2 frequenze risultanti da questa analisi.

Il calcolo diretto è molto laborioso e sono stati sviluppati altri metodi. Il primo sviluppo risale a Blackman e Tukey (1958), che hanno messo in relazione la funzione di autocorrelazione con le stime di varie funzioni spettrali. (La funzione di autocorrelazione r(t) è il coefficiente di correlazione calcolato tra i termini della serie temporale separati da un intervallo di tempo t). Questo metodo era appropriato per le strutture di calcolo a bassa potenza degli anni '50 e '60, ma ora è stato generalmente sostituito dalla cosiddetta trasformata rapida di Fourier (FFT), che sfrutta le proprietà generali di un computer digitale per accelerare notevolmente i calcoli.

La principale limitazione del metodo è che la serie temporale deve contenere 2^k termini, dove k è un numero intero. In generale, questo non è un problema serio, poiché nella maggior parte dei casi ci sono dati sufficienti per organizzare convenientemente la serie a tale lunghezza. In alternativa, alcuni programmi informatici FFT possono utilizzare un numero arbitrario di termini e aggiungere dati sintetici per arrivare a \(2^{k}\) .

Poiché la serie temporale ha una durata finita (N termini), rappresenta solo un campione del segnale di interesse. Pertanto, i coefficienti di Fourier sono solo una stima del valore vero, o della popolazione.

Per migliorare l'affidabilità, è prassi comune fare una media di un numero di termini per ogni lato di una particolare frequenza e assegnare questa media al valore di tale frequenza. In questo modo l'intervallo di confidenza della stima si restringe. Come regola empirica, si suggerisce che 30 gradi di libertà siano un numero soddisfacente per scopi pratici. Pertanto, poiché ogni stima effettuata durante la trasformata di Fourier ha 2 gradi di libertà (associati ai coefficienti dei termini seno e coseno), di solito vengono mediati circa 15 termini. Si noti che 16 è un numero migliore se si utilizza un approccio FFT, poiché è \(2^{4}\) e ci sono esattamente \(2k/24 (= 2^{k-4})\) stime spettrali; ad esempio, se ci sono 1 024 termini nella serie temporale (quindi k = 10), ci saranno 512 stime degli As e dei Bs, e \(64 (= 2^{10-4})\) stime smussate.

L'uso di queste analisi è sempre più parte integrante dei sistemi meteorologici e non riguarda solo l'analisi dei dati. La forma esatta degli spettri che si incontrano in meteorologia può presentare un'ampia gamma di forme. Come si può immaginare, i contributi possono andare dalle frequenze più basse associate ai cambiamenti climatici, ai contributi annuali e stagionali, agli eventi sinottici con periodi di giorni, ai contributi diurni e semidiurni e agli eventi locali a mesoscala fino alla turbolenza e alle variazioni molecolari. Per la maggior parte delle applicazioni meteorologiche, compresa l'analisi sinottica, l'interesse è compreso tra i minuti e i secondi. Lo spettro a queste frequenze diminuisce in genere molto rapidamente con la frequenza. Per periodi inferiori a 1 minuto, lo spettro assume spesso valori proporzionali a n - 5/3. Pertanto, il contributo delle frequenze superiori a 1 Hz è spesso relativamente scarso.

Una delle proprietà importanti dello spettro è che:

\[\sum_{j=0}^{\infty} S(n_{j}) = \sigma^{2}\]

dove σ^2 è la varianza della grandezza misurata. Spesso è conveniente, per l'analisi, esprimere lo spettro in forma continua, in modo che l'equazione 2.4 diventi:

\[\int_{0}^{\infty }S(n)dn = \sigma^{2}\]

Dalle equazioni si evince che i cambiamenti causati allo spettro, ad esempio dal sistema strumentale, altereranno il valore di σ^2 e quindi le proprietà statistiche dell'uscita rispetto all'ingresso. Questa può essere una considerazione importante nella progettazione dello strumento e nell'analisi dei dati.

Si noti anche che il lato sinistro dell'equazione 2.5 è l'area sotto la curva nella Figura 2.2. Quest'area, e quindi la varianza, non viene modificata dall'aliasing se la serie temporale è stazionaria, cioè se il suo spettro non cambia da un momento all'altro.

Risposta del sistema strumentale

I sensori, e i circuiti elettronici che possono essere utilizzati con essi e che costituiscono un sistema strumentale, hanno tempi di risposta e caratteristiche di filtraggio che influenzano le osservazioni.

Nessun sistema strumentale meteorologico, o qualsiasi altro sistema strumentale, segue con precisione la grandezza che sta misurando. In generale, non esiste un modo semplice per descrivere la risposta di un sistema, anche se esistono alcune approssimazioni ragionevoli. Le più semplici possono essere classificate come risposte del primo e del secondo ordine. Ciò si riferisce all'ordine dell'equazione differenziale utilizzata per approssimare il modo in cui il sistema risponde. Per un esame dettagliato dei concetti che seguono, ci sono molti riferimenti nei libri di testo di fisica e nella letteratura (si veda MacCready e Jex, 1964).

In un sistema del primo ordine, come un semplice sensore o il più semplice circuito di filtro passa-basso, la velocità di variazione del valore registrato dallo strumento è direttamente proporzionale alla differenza tra il valore registrato dallo strumento e il valore reale della variabile. Pertanto, se il valore vero al tempo t è s(t) e il valore misurato dal sensore è s0(t), il sistema è descritto dall'equazione differenziale del primo ordine:

\[\frac{ds_{0}(t)}{dt} = \frac{s(t)-s_{0}(t)}{T_{I}}\]

dove TI è una costante con la dimensione del tempo, caratteristica del sistema. La risposta di un sistema del primo ordine a una funzione passo-passo è proporzionale a exp(-t/TI), e TI è osservabile come il tempo necessario, dopo una variazione di passo, affinché il sistema raggiunga il 63% della lettura stabile finale. L'equazione 2.6 è valida per molti sensori, come i termometri.

L'anemometro a coppa è uno strumento del primo ordine, con la proprietà speciale che TI non è costante.

Varia con la velocità del vento. Infatti, il parametro s0 TI è chiamato costante di distanza, perché è quasi costante. Come si può notare in questo caso, l'equazione sopra non è più una semplice equazione del primo ordine, poiché ora è non lineare e di conseguenza presenta notevoli problemi nella sua soluzione. Un ulteriore problema è che TI dipende anche dal fatto che le tazze stiano accelerando o rallentando, cioè che il lato destro sia positivo o negativo. Ciò è dovuto al fatto che il coefficiente di resistenza aerodinamica di una coppa è minore se il flusso d'aria è diretto verso la parte anteriore piuttosto che verso quella posteriore.

La banderuola approssima un sistema del secondo ordine perché l'accelerazione della banderuola verso la direzione vera del vento è proporzionale allo spostamento della banderuola dalla direzione vera.

Questa è, ovviamente, la descrizione classica di un oscillatore (ad esempio, un pendolo). Le pale, sia per natura che per progettazione, sono smorzate. Ciò avviene a causa di una forza resistiva proporzionale e contraria alla sua velocità di variazione. Pertanto, l'equazione differenziale che descrive l'azione della paletta è:

\[\frac{d^{2}\phi_{0}(t)}{dt^{2}} = k_{1}\left[ \phi_{0}(t) - \phi(t) \right] -k_{2}\frac{d\phi_{0}(t)}{dt}\]

dove ϕ è la direzione vera del vento; ϕ0 è la direzione della banderuola; e k1 e k2 sono costanti. La soluzione è un'oscillazione smorzata alla frequenza naturale della banderuola (determinata dalla costante k 1 ). Lo smorzamento è ovviamente molto importante; è controllato dalla costante k2 . Se è troppo piccola, la banderuola oscillerà semplicemente alla frequenza naturale; se è troppo grande, la banderuola non risponderà ai cambiamenti di direzione del vento.

È istruttivo considerare come questi due sistemi rispondono a una variazione graduale del loro ingresso, poiché questo è un esempio del modo in cui gli strumenti rispondono nel mondo reale. Le due equazioni precedenti possono essere risolte analiticamente per questo ingresso. Le risposte sono mostrate nelle due Figure successive.

Si noti che in nessuno dei due casi il sistema misura il valore reale dell'elemento. Inoltre, la scelta dei valori delle costanti k1 e k2 può avere un grande effetto sulle uscite.

Una proprietà importante di un sistema strumentale è la sua funzione di risposta in frequenza o funzione di trasferimento H(n). Questa funzione indica la quantità di spettro trasmessa dal sistema.

Può essere definita come:

\[S(n)_{out} = H(n)S(n)_{in}\]

dove i pedici si riferiscono agli spettri di ingresso e di uscita. Si noti che, in virtù della relazione dell'equazione 2.5, la varianza dell'uscita dipende da H(n). H(n) definisce l'effetto del sensore come filtro, come discusso nella sezione successiva. I modi in cui può essere calcolato o misurato sono illustrati nel paragrafo determinazione delle caratteristiche del sistema.

I filtri

Questa sezione illustra le proprietà dei filtri, con esempi dei modi in cui possono influenzare i dati.

Il filtraggio è l'elaborazione di una serie temporale (continua o discreta, cioè campionata) in modo tale che il valore assegnato in un determinato momento sia ponderato dai valori che si sono verificati in un altro momento.

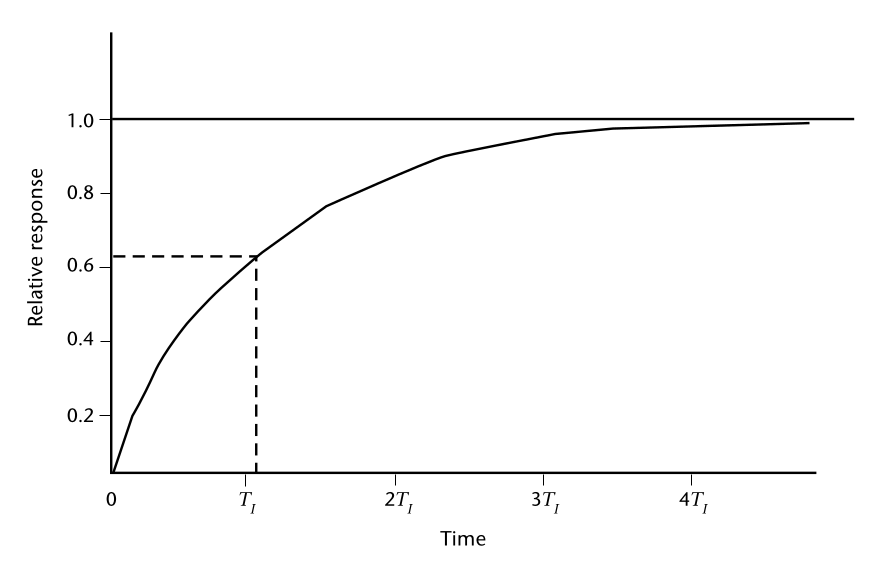
La risposta di un sistema del primo ordine a una funzione a gradino. Al tempo TI il sistema ha raggiunto il 63% del suo valore finale.

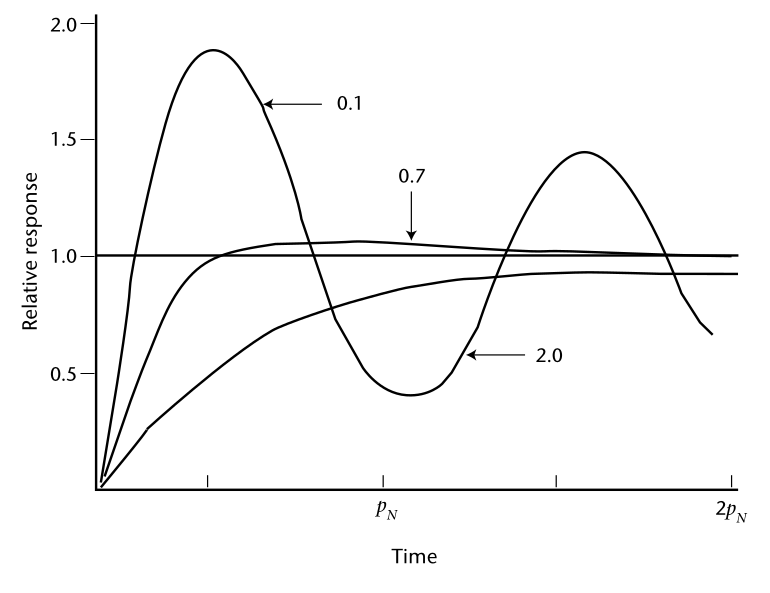
La risposta di un sistema del secondo ordine a una funzione a gradino. pN è il periodo naturale, legato a k1 nell'equazione 2.7, che, per una banderuola, dipende dalla velocità del vento. Le curve mostrate si riferiscono a fattori di smorzamento con valori di 0,1 (smorzamento molto leggero), 0,7 (smorzamento critico, ottimale per la maggior parte degli scopi) e 2,0 (smorzamento forte). Il fattore di smorzamento è correlato a k2 nell'equazione 2.7

Nella maggior parte dei casi, questi orari saranno adiacenti all'ora indicata. Ad esempio, in una serie temporale discreta di N campioni numerati da 0 a N, con valore yi , il valore dell'osservazione filtrata ӯi può essere definito come:

\[\overline{y_{i}} = \sum_{J=-m}^{m}w_{j}y_{i+j}\]

Qui ci sono 2m + 1 termini nel filtro, numerati dalla variabile dummy j da -m a +m, e ӯi è centrato su j = 0. Alcuni dati vengono scartati all'inizio e alla fine del tempo di campionamento. wj è comunemente chiamata funzione di ponderazione e tipicamente è:

\[\sum_{J=-m}^{m}w_{j} = 1\]

in modo che almeno il valore medio della serie filtrata abbia lo stesso valore di quella originale.

L'esempio precedente utilizza il filtraggio digitale. Effetti simili possono essere ottenuti con l'elettronica (ad esempio, con un circuito di resistenze e condensatori) o con le caratteristiche del sensore (ad esempio, come nel caso dell'anemometro, discusso in precedenza). Che sia digitale o analogico, un filtro è caratterizzato da H(n). Se digitale, H(n) può essere calcolato; se analogico, può essere ottenuto con i metodi descritti al punto 2.3.

Ad esempio, si confronti un sistema del primo ordine con un tempo di risposta di TI , e un filtro "box car" di lunghezza Ts su una serie temporale discreta prelevata da un sensore con una risposta molto più rapida. Le forme di questi due filtri sono mostrate nella Figura successiva. Nel primo, è come se lo strumento avesse una memoria che è più forte nell'istante presente, ma che diminuisce esponenzialmente quanto più i dati sono lontani nel tempo. Il filtro box car ha tutti i pesi di uguale entità per il periodo T s e zero oltre. Le funzioni di risposta in frequenza, H(n), per questi due filtri sono mostrate nella Figura 2.6.

Nella figura, le frequenze sono state scalate per mostrare la somiglianza delle due funzioni di risposta. La figura mostra che uno strumento con un tempo di risposta, ad esempio, di 1 s ha approssimativamente lo stesso effetto su un ingresso di un filtro box car applicato per 4 s.

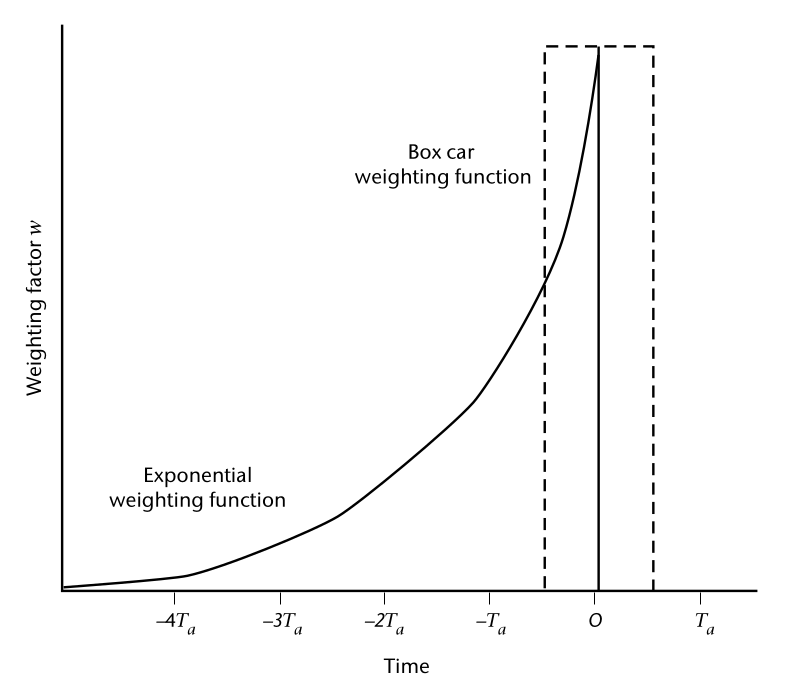
I fattori di ponderazione per una funzione di ponderazione del primo ordine (esponenziale) e per una funzione di ponderazione del box auto. Per il box car Ta è Ts , il tempo di campionamento, e w = 1/N. Per la funzione del primo ordine Ta è TI , la costante di tempo del filtro, e w(t) = (1/TI) exp (-t/TI).

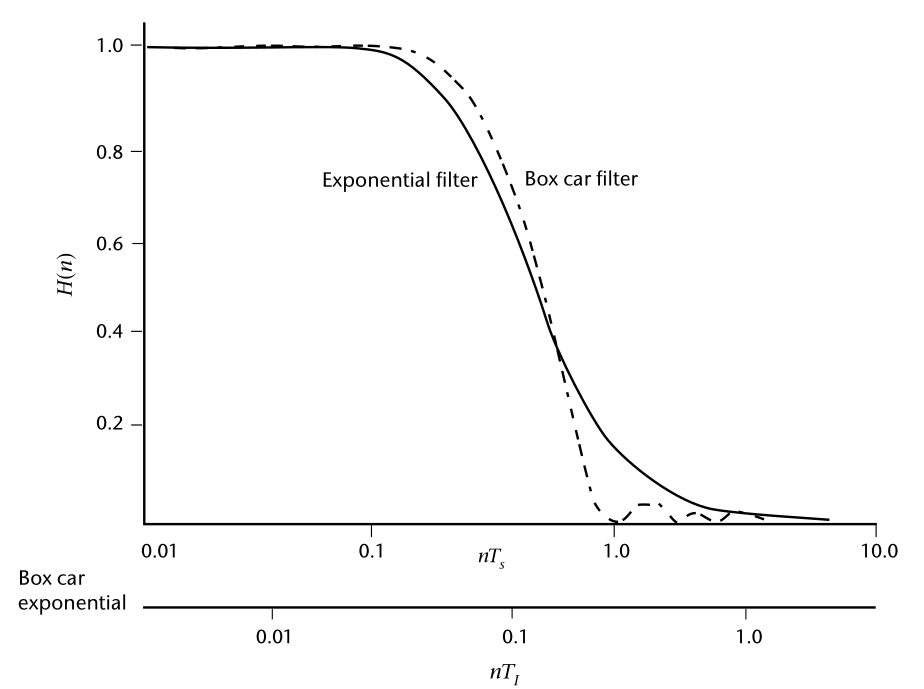
Funzioni di risposta in frequenza per una funzione di ponderazione del primo ordine (esponenziale) e una funzione di ponderazione box car. La frequenza è normalizzata per il filtro del primo ordine da T I, la costante di tempo, e per il filtro box car da T s, il tempo di campionamento.

Tuttavia, va notato che un filtro box car, che viene calcolato numericamente, non si comporta in modo semplice. Non rimuove tutte le frequenze più alte oltre la frequenza di Nyquist e può essere utilizzato validamente solo se lo spettro cade rapidamente al di sopra di n y . Si noti che il filtro box car mostrato nella Figura 2.6 è una soluzione analitica per w come funzione continua; se il numero di campioni nel filtro è piccolo, il taglio è meno netto e i picchi indesiderati di frequenza superiore sono più grandi.

Si veda Acheson (1968) per consigli pratici sul box car e sul filtraggio esponenziale e per un confronto dei loro effetti.

Nella Figura 2.7 è riportata la funzione di risposta di un sistema del secondo ordine, in questo caso per una banderuola, che mostra come lo smorzamento agisca come un filtro passa-banda.

Si può notare che l'elaborazione dei segnali da parte dei sistemi può avere effetti profondi sui dati in uscita e deve essere eseguita con competenza.

Tra gli effetti dei filtri vi è il modo in cui essi possono modificare le informazioni statistiche dei dati. Uno di questi è stato accennato prima e illustrato nelle equazioni 2.5 e 2.8. L'equazione 2.5 mostra come l'integrale dello spettro su tutte le frequenze dia la varianza della serie temporale, mentre l'equazione 2.8 mostra come il filtraggio, in virtù dell'effetto della funzione di trasferimento, modifichi lo spettro misurato. Si noti che la varianza non sempre diminuisce con il filtraggio. Ad esempio, in alcuni casi, per un sistema del secondo ordine, la funzione di trasferimento amplificherà alcune parti dello spettro ed eventualmente aumenterà la varianza, come mostrato nella Figura 2.7.

Per fare un altro esempio, se la distribuzione è gaussiana, la varianza è un parametro utile. Se fosse diminuita dal filtraggio, un utente dei dati sottostimerebbe l'allontanamento dalla media degli eventi che si verificano con determinate probabilità o periodi di ritorno.

Inoltre, la progettazione del filtro digitale può avere effetti indesiderati o inaspettati. Se si esamina la Figura 2.6, si può notare che la funzione di risposta del filtro box car presenta una serie di massimi a frequenze superiori a quella in cui diventa zero. Ciò conferisce ai dati filtrati una piccola periodicità a queste frequenze. In questo caso, l'effetto sarà minimo poiché i massimi sono piccoli. Tuttavia, per alcuni progetti di filtro possono essere introdotti dei massimi piuttosto significativi. Come regola generale, minore è il numero di pesi, maggiore è il problema. In alcuni casi, sono state rilevate periodicità nei dati che esistevano solo perché i dati erano stati filtrati.

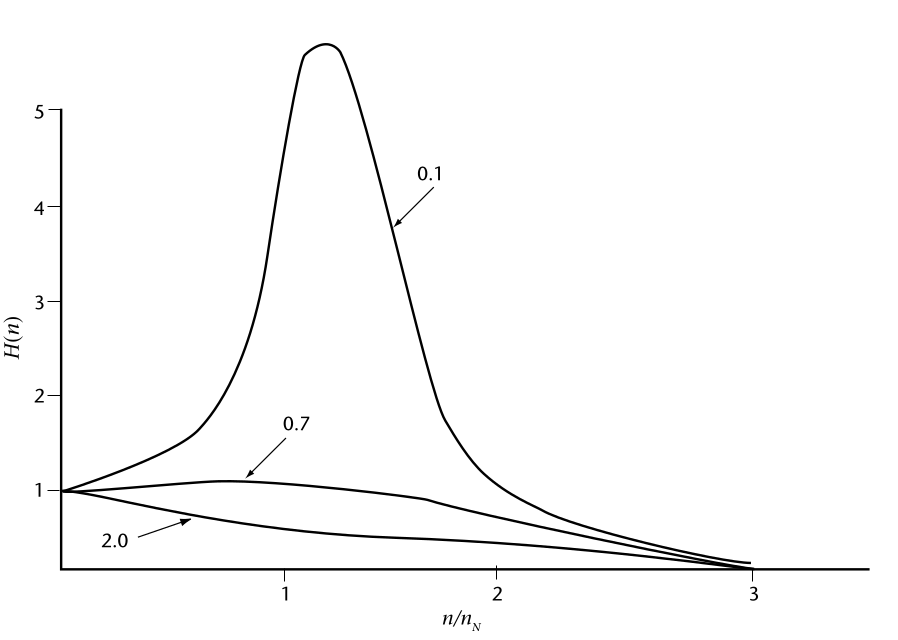
Funzioni di risposta in frequenza per un sistema del secondo ordine, come una banderuola. La frequenza è normalizzata da n N, la frequenza naturale, che dipende dalla velocità del vento. Le curve mostrate si riferiscono a fattori di smorzamento con valori di 0,1 (smorzamento molto leggero), 0,7 (smorzamento critico, ottimale per la maggior parte degli scopi) e 2,0 (smorzamento forte).

Un problema legato al concetto di filtro è la lunghezza del campione. Questo può essere illustrato osservando che, se la lunghezza della registrazione è di durata T, contributi alla variabilità dei dati a frequenze inferiori a 1/T non saranno possibili. Si può dimostrare che una registrazione finita ha una durata di 1/T. Si può dimostrare che una lunghezza di registrazione finita ha l'effetto di un filtro passa-alto. Come per i filtri passa-basso discussi in precedenza, anche un filtro passa-alto avrà un impatto sulle statistiche dei dati in uscita.

Determinazione delle caratteristiche del sistema

Le caratteristiche di filtraggio di un sensore o di un circuito elettronico, o del sistema che li compone, devono essere note per determinare la frequenza di campionamento appropriata per le serie temporali che il sistema produce. La procedura consiste nel misurare la funzione di trasferimento o di risposta H(n) di cui all'equazione 2.8. La funzione di trasferimento può essere ottenuta in almeno tre modi: tramite misurazione diretta, calcolo e stima.

Misura diretta della risposta

La risposta può essere misurata direttamente con almeno due metodi. Nel primo metodo si applica al sensore o al filtro una variazione nota, ad esempio una funzione a gradino, e si misura il suo tempo di risposta; si può quindi calcolare H(n). Nel secondo metodo, l'uscita del sensore viene confrontata con un altro sensore molto più veloce. Il primo metodo è più comunemente utilizzato del secondo.

Un semplice esempio di come determinare la risposta di un sensore a un ingresso noto è la misurazione della costante di distanza di un anemometro a tazza rotante o a elica. In questo esempio, l'ingresso noto è una funzione a gradini. L'anemometro viene posto in un flusso d'aria a velocità costante, gli viene impedito di ruotare, quindi viene rilasciato e la sua uscita viene registrata. Il tempo impiegato dall'uscita per passare da zero al 63% della velocità finale o di equilibrio nel flusso d'aria è il tempo "costante".

Se è disponibile un altro sensore che risponde molto più rapidamente di quello di cui si vuole determinare la risposta, è possibile misurare e confrontare con buona approssimazione sia l'ingresso che l'uscita. Il dispositivo più semplice da utilizzare per effettuare il confronto è probabilmente un moderno analizzatore di spettro digitale a due canali. L'uscita del sensore a risposta rapida viene immessa in un canale, l'uscita del sensore da testare nell'altro canale e la funzione di trasferimento viene visualizzata automaticamente.

La funzione di trasferimento è una descrizione diretta del sensore come filtro. Se il dispositivo di cui si vuole determinare la risposta è un circuito elettronico, generare un ingresso noto o addirittura veramente casuale è molto più facile che trovare un sensore molto più veloce. Anche in questo caso, un moderno analizzatore di spettro digitale a due canali è probabilmente il più conveniente, ma è possibile utilizzare altri strumenti di test elettronici.

Calcolo della risposta

È l'approccio descritto al punto 2.2.3. Se si conosce a sufficienza la fisica di un sensore/filtro, la risposta a una grande varietà di ingressi può essere determinata mediante una soluzione analitica o numerica. È possibile calcolare sia la risposta a ingressi specifici, come una funzione a gradini, sia la funzione di trasferimento. Se il sensore o il circuito è lineare (descritto da un'equazione differenziale lineare), la funzione di trasferimento è una descrizione completa, in quanto descrive le risposte in ampiezza e fase in funzione della frequenza, in altre parole, come un filtro. Considerare la risposta in funzione della frequenza non è sempre conveniente, ma la funzione di trasferimento ha una controparte in trasformata di Fourier, la funzione di risposta all'impulso, che rende molto più semplice l'interpretazione della risposta in funzione del tempo. Le figure 2.3 e 2.4 illustrano la risposta in funzione del tempo.

Se possibile, le soluzioni analitiche sono preferibili perché mostrano chiaramente la dipendenza dai vari parametri.

Stima della risposta

Se le funzioni di trasferimento di un trasduttore e di ogni circuito successivo sono note, il loro prodotto è la funzione di trasferimento dell'intero sistema. Se, come di solito accade, le funzioni di trasferimento sono filtri passa-basso, la funzione di trasferimento aggregata è un filtro passa-basso la cui frequenza di taglio è inferiore a quella dei singoli filtri.

Se una delle frequenze di taglio individuali è molto inferiore a quella degli altri, la frequenza di taglio dell'aggregato è solo leggermente inferiore.

Poiché la frequenza di taglio di un filtro passa-basso è approssimativamente l'inverso della sua costante di tempo, ne consegue che, se una delle costanti di tempo individuali è molto più grande di qualsiasi altra, la costante di tempo dell'aggregato è solo leggermente più grande.

Campionamento

Tecniche di campionamento

Lo schema successivo illustra schematicamente un tipico sensore e circuito di campionamento. Quando è esposto all'atmosfera, alcune proprietà del trasduttore cambiano in funzione di una variabile atmosferica come la temperatura, la pressione, la velocità o la direzione del vento o l'umidità e converte tale variabile in un segnale utile, solitamente elettrico. I circuiti di condizionamento del segnale svolgono comunemente funzioni quali la conversione dell'uscita del trasduttore in tensione, l'amplificazione, la linearizzazione, la compensazione e lo smussamento. Il filtro passa-basso finalizza l'uscita del sensore per l'ingresso sample-and-hold. Il sample-and-hold e il convertitore analogico-digitale producono i campioni da cui viene calcolata l'osservazione nel processore.

Va notato che lo smussamento eseguito nello stadio di condizionamento del segnale per ragioni ingegneristiche, per eliminare i picchi e stabilizzare l'elettronica, viene eseguito da un filtro passa-basso; esso riduce il tempo di risposta del sensore e rimuove le alte frequenze che possono essere di interesse. Il suo effetto deve essere esplicitamente compreso dal progettista e dall'utente e la sua frequenza di taglio deve essere la più alta possibile.

I cosiddetti “sensori intelligenti”, quelli dotati di microprocessore, possono incorporare tutte le funzioni illustrate. Il circuito di condizionamento del segnale può non essere presente in tutti i sensori, oppure può essere combinato con altri circuiti. In altri casi, come nel caso di un anemometro a tazza rotante o a elica, può essere facile parlare solo di un sensore perché è difficile distinguere un trasduttore. Nei pochi casi in cui l'uscita di un trasduttore o di un sensore è un segnale la cui frequenza varia con la variabile atmosferica misurata, il sample-and-hold e il convertitore analogico-digitale possono essere sostituiti da un contatore. Ma questi non sono dettagli importanti. L'elemento importante nella progettazione è garantire che la sequenza di campioni rappresenti adeguatamente le variazioni significative della variabile atmosferica da misurare.

La prima condizione imposta ai dispositivi illustrati nella Figura 2.8 è che il sensore deve rispondere abbastanza rapidamente da seguire le fluttuazioni atmosferiche che devono essere descritte nell'osservazione. Se l'osservazione deve essere una media di 1, 2 o 10 minuti, questo non è un requisito molto impegnativo. Se invece l'osservazione deve riguardare una caratteristica della turbolenza, come un picco di vento, è necessario prestare attenzione nella scelta del sensore.

An instrument system

Atmosphere
   |
SENSOR/TRANSDUCER
   |
SIGNAL CONDITIONING CIRCUITS
   |
LOW-PASS FILTER
   |
SAMPLE-AND-HOLD
   |                 CLOCK
ANALOGUE-TO-DIGITAL CONVERTER
   |
PROCESSOR
   |
Observation

La seconda condizione imposta ai dispositivi illustrati nella Figura è che il sample-and-hold e il convertitore analogico-digitale devono fornire un numero di campioni sufficiente per effettuare una buona osservazione. L'accuratezza richiesta dalle osservazioni meteorologiche di solito mette alla prova il sensore, non la tecnologia di campionamento elettronico. Tuttavia, il sensore e il campionamento devono essere abbinati per evitare l'aliasing. Se la frequenza di campionamento è limitata per motivi tecnici, il sistema sensore-filtro deve essere progettato per eliminare le frequenze che non possono essere rappresentate.

Se il sensore ha una funzione di risposta adeguata, il filtro passa-basso può essere omesso,incluso solo come assicurazione, o può essere incluso perché migliora la qualità del segnale in ingresso al sample-and-hold. Ad esempio, un filtro di questo tipo può essere incluso per eliminare il rumore all'estremità di un cavo lungo o per rendere più uniforme l'uscita del sensore. Ovviamente, questo circuito deve anche rispondere in modo sufficientemente rapido da seguire le fluttuazioni atmosferiche di interesse.

Frequenza di campionamento

Per la maggior parte delle applicazioni meteorologiche e climatologiche, le osservazioni sono richieste a intervalli da 30 minuti a 24 ore e ogni osservazione viene effettuata con un tempo di campionamento dell'ordine di 1-10 minuti. Il Volume I, Capitolo 1, Allegato 1.A fornisce una dichiarazione recente dei requisiti per questi scopi.

Una pratica comune per le osservazioni di routine consiste nell'effettuare una lettura spot del sensore (ad esempio un termometro) e affidarsi alla sua costante di tempo per fornire un tempo di campionamento approssimativamente corretto.

Ciò equivale a utilizzare un filtro esponenziale (Figura 2.6). I sistemi nelle stazioni meteorologiche automatiche utilizzano comunemente sensori più veloci e devono essere effettuate diverse letture spot ed elaborate per ottenere una media (filtro box car) o un'altra media adeguatamente ponderata.

Uno schema pratico consigliato per le frequenze di campionamento è il seguente:

1. I campioni prelevati per calcolare le medie devono essere ottenuti a intervalli di tempo equidistanti che:

   1. non superino la costante di tempo del sensore; oppure

   2. non superino la costante di tempo di un filtro analogico passa-basso che segue l'uscita linearizzata di un sensore a risposta rapida; oppure linearizzato di un sensore a risposta rapida; oppure

   3. sono in numero sufficiente a garantire che l'incertezza della media dei campioni sia ridotta a un livello accettabile, per esempio, inferiore all'accuratezza richiesta della media; (iii) sono in numero sufficiente a garantire che l'incertezza della media sia ridotta a un livello accettabile, per esempio, inferiore all'accuratezza richiesta della media.

2. I campioni da utilizzare per stimare le fluttuazioni estreme, come le raffiche di vento, devono essere prelevati con una frequenza almeno quattro volte superiore a quella specificata ai punti (i) o (ii).

Per ottenere le medie, sono spesso raccomandate e praticate frequenze di campionamento un po' più rapide di (i) e (ii), come due volte per costante di tempo.

I criteri (i) e (ii) derivano dalla considerazione della frequenza di Nyquist. Se la spaziatura di campionamento Δt ≤ T I , la frequenza di campionamento n ≥ 1/TI e nT I ≥ 1. Dalla curva esponenziale della Figura 2.6 si può notare che in questo modo si eliminano le frequenze più alte e si evita l'aliasing. Se Δt = T I , n y = 1/2T I e i dati saranno falsati solo dall'energia spettrale alle frequenze di nT I = 2 e oltre, cioè dove le fluttuazioni hanno periodi inferiori a 0,5T I .

I criteri (i) e (ii) sono utilizzati per il campionamento automatico. Il criterio statistico in (iii) è più applicabile alle frequenze di campionamento molto più basse delle osservazioni manuali. L'incertezza della media è inversamente proporzionale alla radice quadrata del numero di osservazioni e il suo valore può essere determinato dalle statistiche della grandezza.

Il criterio (b) sottolinea la necessità di alte frequenze di campionamento, o più precisamente di piccole costanti di tempo, per misurare le raffiche. Le raffiche registrate sono smussate dalla risposta dello strumento e il massimo registrato sarà mediato su diverse volte la costante di tempo.

L'effetto dell'aliasing sulle stime della media può essere visto molto semplicemente considerando ciò che accade quando la frequenza dell'onda misurata è uguale alla frequenza di campionamento, o un suo multiplo. La media derivata dipenderà dalla tempistica del campionamento. Un campione ottenuto una volta al giorno a un'ora fissa non fornirà una buona stima della temperatura media mensile.

Per un'illustrazione un po' più complessa dell'aliasing, si consideri una serie temporale di osservazioni della temperatura effettuate ogni tre ore con un normale termometro. Se la temperatura varia dolcemente nel tempo, come accade di solito, la media giornaliera calcolata da otto campioni è accettabilmente stabile.

Tuttavia, se si è verificato un evento a mesoscala (un temporale) che ha ridotto la temperatura di molti gradi per 30 minuti, la media calcolata è errata. L'affidabilità delle medie giornaliere dipende dalla consueta debolezza dello spettro nella mesoscala e nelle frequenze più alte.

Tuttavia, il verificarsi di un evento a più alta frequenza (il temporale) altera i dati, influenzando il calcolo della media, della deviazione standard e di altre misure di dispersione e dello spettro.

La questione della frequenza di campionamento può essere discussa anche in base alla Figura 2.8. Nel paragrafo 2.2.1 si è detto che, per la misura degli spettri, la frequenza di campionamento, che determina la frequenza di Nyquist, deve essere scelta in modo che lo spettro delle fluttuazioni al di sopra della frequenza di Nyquist sia troppo debole per influenzare lo spettro calcolato. Ciò si ottiene se la frequenza di campionamento impostata dall'orologio nella Figura 2.8 è almeno il doppio della frequenza più alta di ampiezza significativa nel segnale di ingresso al sample-and-hold.

L'espressione “massima frequenza di ampiezza significativa” usata sopra è vaga. È difficile trovare una definizione rigorosa perché i segnali non sono mai veramente limitati nella larghezza di banda. Tuttavia, non è difficile garantire che l'ampiezza delle fluttuazioni del segnale diminuisca rapidamente con l'aumentare della frequenza e che l'ampiezza al quadrato della radice delle fluttuazioni al di sopra di una determinata frequenza sia piccola rispetto al rumore di quantizzazione del convertitore analogico-digitale, piccola rispetto a un livello di errore o di rumore accettabile nei campioni, oppure contribuisca in modo trascurabile all'errore o al rumore totale dell'osservazione.

Nel paragrafo 2.3 sono state illustrate le caratteristiche dei sensori e dei circuiti che possono essere scelti o regolati per garantire che l'ampiezza delle fluttuazioni del segnale diminuisca rapidamente con l'aumentare della frequenza.

La maggior parte dei trasduttori, in virtù della loro incapacità di rispondere alle fluttuazioni atmosferiche rapide (ad alta frequenza) e della loro capacità di riprodurre fedelmente i cambiamenti lenti (a bassa frequenza), sono anche filtri passa-basso. Per definizione, i filtri passa-basso limitano la larghezza di banda e, per il teorema di Nyquist, limitano anche la frequenza di campionamento necessaria per riprodurre accuratamente l'uscita del filtro. Ad esempio, se ci sono variazioni reali nell'atmosfera con periodi fino a 100 ms, la frequenza di campionamento di Nyquist sarebbe di 1 ogni 50 ms, il che è tecnicamente impegnativo. Tuttavia, se vengono osservate attraverso un sensore e un filtro che rispondono molto più lentamente, ad esempio con una costante di tempo di 10 s, la frequenza di campionamento di Nyquist sarebbe di 1 campione ogni 5 s, molto più semplice ed economica, e preferibile se non sono richieste misure delle alte frequenze.

Frequenza di campionamento e controllo di qualità

Molte tecniche di controllo della qualità dei dati utilizzate negli AWS dipendono dalla coerenza temporale, o persistenza, dei dati per la loro efficacia. A titolo di esempio molto semplice, è opportuno prendere in considerazione due ipotetici algoritmi di controllo della qualità per le misure di pressione nei SAR. I campioni vengono prelevati ogni 10 s e le medie di 1 minuto vengono calcolate ogni minuto. Si presume che la pressione atmosferica cambi solo raramente, se non mai, a una velocità superiore a 1 hPa al minuto.

Il primo algoritmo rifiuta la media se differisce dalla precedente di più di 1 hPa. In questo modo non si farebbe un buon uso dei dati disponibili. Permette a un singolo campione con un errore di 6 hPa di passare inosservato e di introdurre un errore di 1 hPa in un'osservazione.

Il secondo algoritmo rifiuta un campione se differisce dal precedente per più di 1 hPa. In questo caso, una media non contiene errori superiori a circa 0,16 (1/6) hPa. In realtà, se l'ipotesi è corretta e cioè che la pressione atmosferica cambia solo raramente a una velocità superiore a 1 hPa al minuto, i criteri di accettazione/rifiuto dei campioni adiacenti potrebbero essere ridotti a 0,16 hPa e l'errore nella media potrebbe essere ancora più ridotto.

Il punto dell'esempio è che le procedure di controllo della qualità dei dati che dipendono dalla coerenza temporale (correlazione) per la loro efficacia si applicano meglio ai dati ad alta risoluzione temporale (frequenza di campionamento). All'estremità delle alte frequenze dello spettro nell'uscita del sensore/filtro, la correlazione tra campioni adiacenti aumenta con l'aumentare della frequenza di campionamento fino a raggiungere la frequenza di Nyquist, dopo la quale non si verifica un ulteriore aumento della correlazione.

Fino a questo punto della discussione, non è stato detto nulla che scoraggi l'uso di un sensore/filtro con una costante di tempo, purché il periodo di mediazione richiesto per l'osservazione sia preso come un singolo campione da usare come osservazione. Sebbene le esigenze del sottosistema digitale siano minime, è necessaria un'altra considerazione per un efficace controllo della qualità dei dati. Le osservazioni possono essere raggruppate nelle tre categorie seguenti:

1. Accurate (osservazioni con errori inferiori o uguali a un valore specificato);

2. Inaccurate (osservazioni con errori superiori a un valore specificato);

3. mancanti.

Il controllo della qualità dei dati ha due ragioni: ridurre al minimo il numero di osservazioni imprecise e ridurre al minimo il numero di osservazioni mancanti. Per raggiungere entrambi gli obiettivi è necessario garantire che ogni osservazione sia calcolata da un numero ragionevolmente elevato di campioni controllati per la qualità dei dati. In questo modo, è possibile isolare ed escludere i campioni con errori spuri di grandi dimensioni e il calcolo può comunque procedere senza essere contaminato da quel campione.

Ulteriore approfondimento: https://web.stanford.edu/class/engr76/lectures/lecture9-10.pdf

Errore standard

Derivato da un'opera di: Andrea Minini - email: info@andreaminini.com - PEC andreaminini@pec.it

licenza CC BY 4.0 Attribution 4.0 International https://creativecommons.org/licenses/by/4.0/

L'errore standard ex rappresenta la deviazione standard della media campionaria, ovvero quanto ci si aspetta che la media E(X) calcolata su un campione X differisca dalla vera media μ della popolazione.

L'errore standard è dato dalla formula:

\[e_{x}=\frac{\sigma}{\sqrt{n}}\]

Dove:

• σ è la deviazione standard della popolazione, cioè una misura della dispersione dei dati nella popolazione.

• n è la dimensione del campione, cioè il numero di osservazioni raccolte dal campione.

Se la media campionaria è E(X), allora si posso ragionevolmente affermare che la media della popolazione μ si trova approssimativamente all'interno dell'intervallo

E(X)±ex

Dalla formula

\[e_{x}=\frac{\sigma}{\sqrt{n}}\]

deduco che all'aumentare della dimensione del campione n l'errore standard diminuisce.

Questo avviene perché con campioni più grandi la media campionaria tende a essere più vicina alla media reale della popolazione.

Stima

La deviazione standard σ della popolazione campionata è raramente nota. Pertanto, l'errore standard della media viene solitamente stimato sostituendo σ con la deviazione standard σx del campione:

\[e_{x}\sim \frac{\sigma_{x}}{\sqrt{n}}\]

Esempio di campionamento

Questo un esempio di campionamento di temperatura con la retta di regressione lineare:

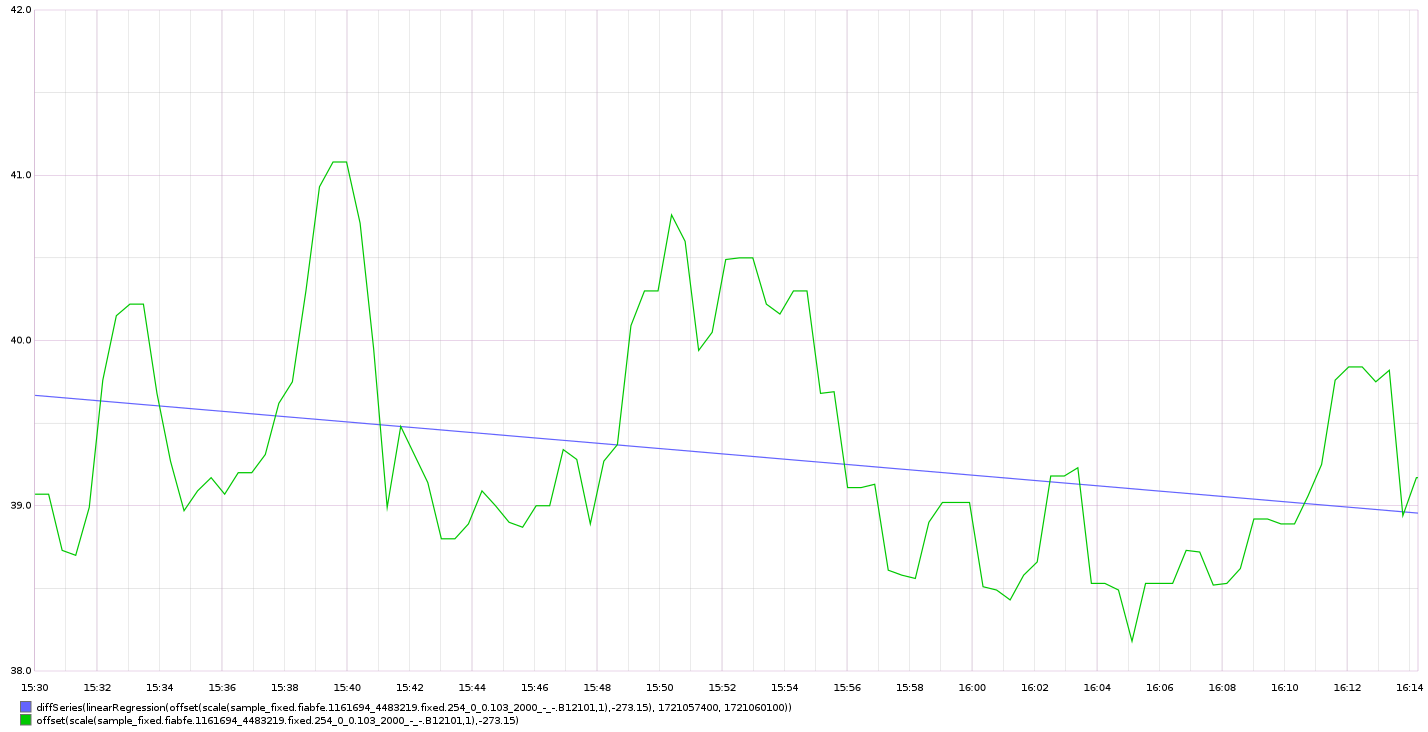
come ordine di grandezza si deduce che campionando ogni 30 secondi l'errore sulla temperatura media oraria è dell'ordine di grandezza del decimo di grado con campionamneti ogni 30 secondi

\[0.09 = \frac{1}{\sqrt{120}}\]

Qui alcune considerazioni sulla costante di tempo: https://www.unirc.it/documentazione/materiale_didattico/597_2011_289_11765.pdf pdf

Taratura e calibrazione

la taratura è un'operazione che permette di definire le caratteristiche metrologiche di uno strumento, allo scopo di definirne la precisione; la calibrazione ha come obiettivo quello di rendere lo strumento più accurato e spesso, conseguentemente, migliorarne la precisione

La taratura

La taratura può essere usata per la determinazione delle caratteristiche metrologiche dello strumento (es. accuratezza, ripetibilità, riproducibilità, linearità, ecc.) necessari per definirne la funzionalità, o per verificarne la rispondenza a dei requisiti. Inoltre permette di sapere qual è la variazione del valore della grandezza.

Curva di taratura

Una curva di taratura è una funzione di trasferimento che collega l'ingresso all'uscita. Il metodo si basa sul rapporto proporzionale tra la concentrazione e un dato segnale analitico (proprietà).

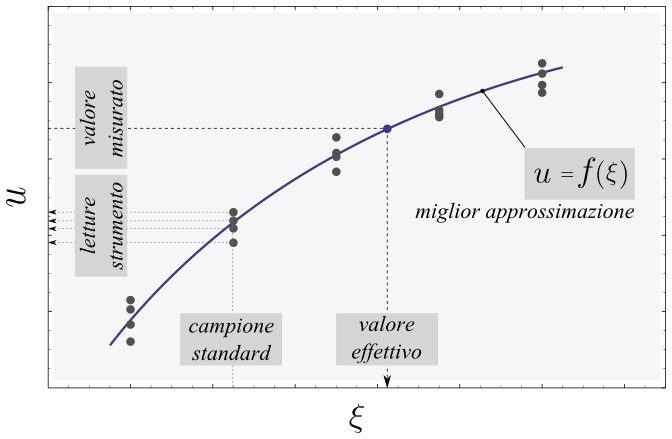
La calibrazione

L'insieme di operazioni svolte su un sistema di misura, affinché esso fornisca indicazioni prescritte in corrispondenza di determinati valori di una grandezza da sottoporre a misurazione

La calibrazione consiste nel confrontare i valori ottenuti da uno strumento di misura con la corrispondente misura di uno strumento di riferimento (o standard). Secondo l'Ufficio internazionale dei pesi e delle misure, la calibrazione è "un'operazione che, in condizioni specifiche, stabilisce in una prima fase una relazione tra i valori e le incertezze di misura provviste di standard e indicazioni corrispondenti alle incertezze di misura associate e in una seconda fase, utilizza queste informazioni per stabilire un rapporto per ottenere un risultato di misura da un'indicazione".

Da questa definizione si può dedurre che per calibrare uno strumento o uno standard è necessario uno strumento con una maggiore precisione (riferimento) che fornisca il valore convenzionale (misure di riferimento)

Metodologia

A confronto, dove una medesima grandezza viene contemporaneamente letta dallo strumento in calibrazione e da quello campione; a sostituzione, dove il campione genera direttamente la grandezza di riferimento che viene fatta misurare allo strumento in calibrazione;

La validazione dei dati

Per validazione dei dati si intende «il processo attraverso il quale si valuta se l’informazionepuò essere considerata consona alle finalità per le quali è stata prodotta» (ISTAT, 2001).

L’attività di validazione può essere allora definita, sempre secondo l’ISTAT, come «l’insiemedelle operazioni attraverso le quali si giudica lo scarto esistente fra gli obiettivi di qualità programmati in sede di progettazione dell’indagine [...] e i risultati effettivamente conseguiti».

http://www.isprambiente.gov.it/contentfiles/00003800/3874-rapporti-02-27.pdf/

pdf

Misure meteorologiche

Criteri generali per la scelta del sito

La stazione meteorologica deve sorgere in un luogo piano e libero, possibilmente il suolo deve essere coperto da un tappeto erboso da cui vanno eliminate erbacce e cespugli. Il taglio della copertura erbosa deve essere frequente in modo da tenere l'erba uniformemente bassa; l'erba tagliata deve essere asportata per evitare l'effetto pacciamante della stessa e le conseguenti modificazioni del regime di temperatura ed umidità del terreno. E' sempre sconsigliabile lastricare di cemento o asfaltare o coprire con pietre o ghiaia il terreno del sito; in tale condizione infatti il calore riverberato altera di diversi gradi la temperatura dell'aria falsando le misure. Se non vi fossero altre possibilità , in caso di montaggio su terrazzo si consiglia di predisporre sotto la capannina un ampio riquadro di terreno inerbito contenuto in apposito recipiente . Il parco strumenti dovrebbe situarsi ad una distanza minima pari 4 – 8 volte l'altezza degli ostacoli esistenti (alberi, siepi, edifici, muri etc.). Non devono esistere ostacoli che creino ombra ; brevi periodo di ombreggiamento al sorgere ed al tramontare del sole. La stazione ideale deve essere posta in un luogo realmente rappresentativo delle condizioni naturali della regione agricola o urbana considerata, ma non sempre nella ricerca dei siti per stazioni meteo ambientali è possibile raggiungere il completo rispetto di queste condizioni. In queste condizioni è consigliabile ricercare le migliori condizioni possibili avendo l'accortezza di documentare dettagliatamente le particolarità della collocazione della strumentazione

Temperatura e umidità

Schermi

La capannina meteorologica

La capannina solitamente di legno (scarsa conducibilità termica) e colorata con vernice bianca riflettente (minima assorbimento di radiazione); inoltre è realizzata in modo da garantire la circolazione dell'aria all'interno. Per evitare l'effetto della radiazione infrarossa emessa dal terreno, la capannina deve avere sulla base inferiore una doppia schermatura. La disposizione della capannina, con la porta disposta verso nord, evita che l'insolazione diretta penetri fino ai sensori di temperatura durante l'osservazione / manutenzione.

Istruzioni per la costruzione di una capannina meteorologica

La capannina per gli strumenti deve essere costruito con uno spessore di circa 2 cm di pino bianco o legno simile e dipinto di bianco, sia all'interno che all'esterno. È necessario installare una serratura per impedire la manomissione degli strumenti. All'interno devono essere installati dei blocchi di montaggio per garantire che il termometro max/min non tocchi la parete posteriore. Le parti devono essere avvitate o incollate e inchiodate. I piani sono specificati in unità metriche.

Pertanto, potrebbe essere necessario apportare piccole modifiche alle dimensioni in base alle dimensioni standard del legno nella propria regione. È più facile acquistare pannelli a lamelle prefabbricati, che di solito sono disponibili per l'acquisto. Il criterio principale per la costruzione delle feritoie è quello di garantire la ventilazione della pensilina dello strumento, impedendo al contempo l'ingresso diretto di luce solare e pioggia. Per evitare che la luce del sole penetri nel rifugio, si consiglia di sovrapporre leggermente ogni lamella alle lamelle adiacenti. Vedere la figura:

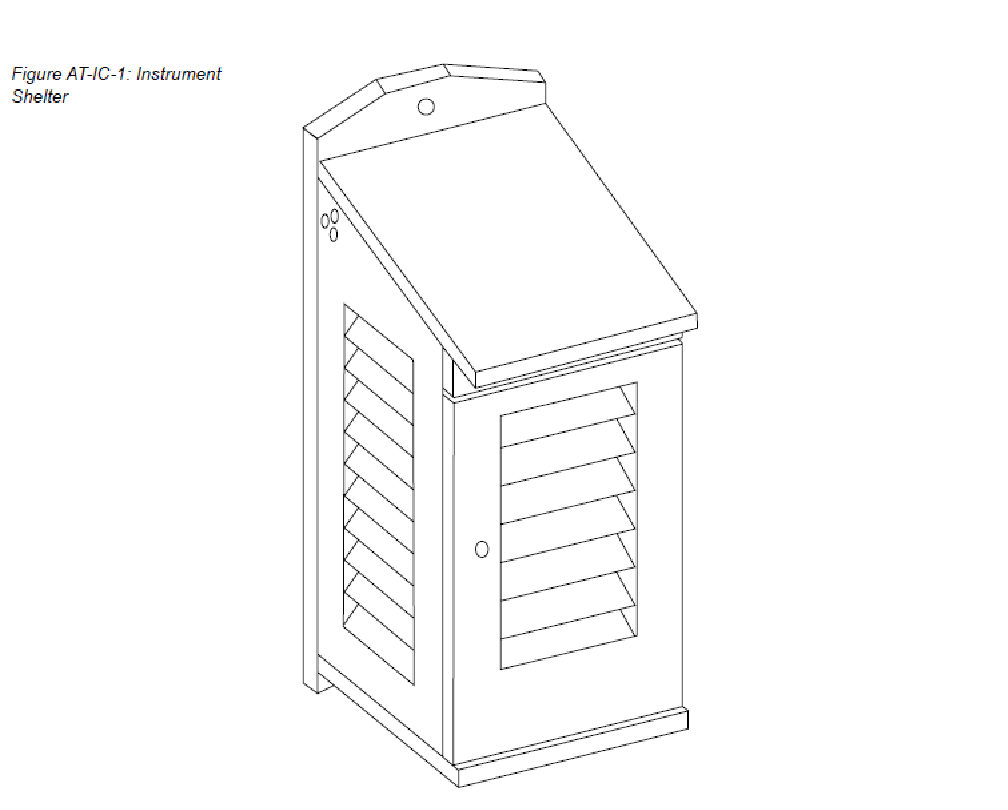
Inoltre, lo spazio tra le lamelle deve essere di circa 1 cm e l'angolo delle lamelle deve essere di circa 50-60 gradi rispetto all'orizzontale. Per le istruzioni di montaggio della pensilina, vedere l'immagine:

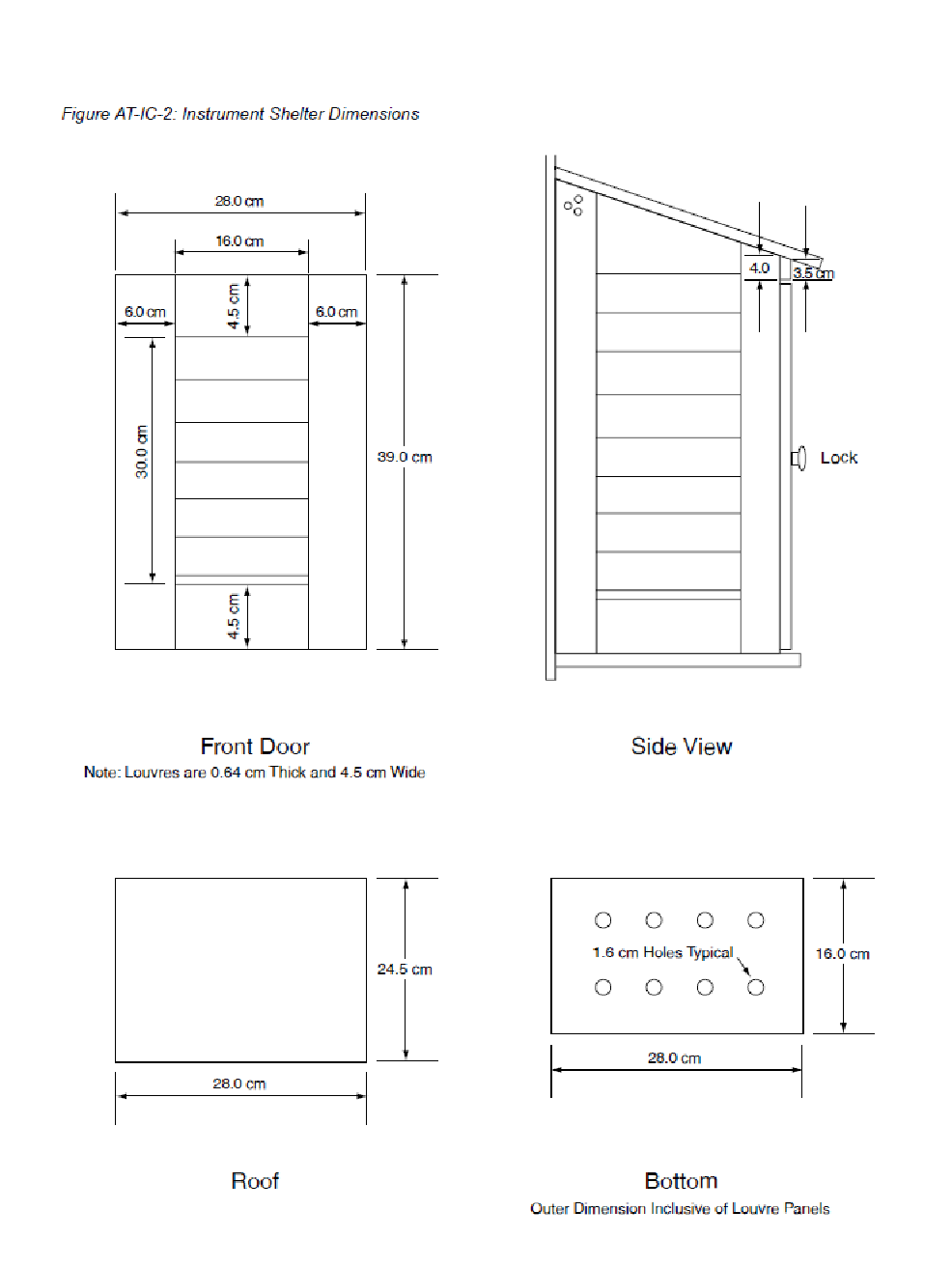
Schermo solare

Lo schermo o la protezione dalle radiazioni deve essere progettato per fornire un involucro con una temperatura interna uniforme e uguale a quella dell'aria esterna. Deve circondare completamente i termometri ed escludere il calore radiante, le precipitazioni e altri fenomeni che potrebbero influenzare la misurazione. Gli schermi con ventilazione forzata, in cui l'aria viene aspirata sull'elemento termometrico da un ventilatore, possono aiutare a evitare distorsioni quando il microclima all'interno dello schermo si discosta dalla massa d'aria circostante. Tale deviazione si verifica solo quando la velocità del vento naturale è molto bassa (< 1 m s-1). Quando si utilizza una ventilazione artificiale di questo tipo, occorre fare attenzione a evitare la deposizione di aerosol e gocce di pioggia sul sensore, che ne riducono la temperatura verso la temperatura di bulbo umido. Come materiale di schermatura, il metallo altamente lucidato e non ossidato è favorevole a causa della sua elevata riflettività e del basso assorbimento di calore. Tuttavia, il materiale termicamente isolante a base di plastica è preferibile per i suoi semplici requisiti di manutenzione. Il materiale termoisolante deve essere utilizzato se il sistema si basa sulla ventilazione naturale.

Schermi a lamelle

La maggior parte delle numerose varietà di schermi a lamelle o piattelli si basa sulla ventilazione naturale. Le pareti di una zanzariera di questo tipo dovrebbero essere preferibilmente a doppia lastra e il pavimento dovrebbe essere costituito da tavole sfalsate, ma è possibile trovare altri tipi di costruzione che soddisfino i requisiti di cui sopra.

Il tetto dovrebbe essere a doppio strato, con disposizioni per la ventilazione dello spazio tra i due strati. Nei climi freddi, a causa dell'elevata riflettività della neve (fino all'88%), lo schermo dovrebbe avere anche un doppio pavimento. Allo stesso tempo, però, il pavimento dovrebbe essere facilmente abbassabile o inclinabile, in modo da poter rimuovere la neve che entra nello schermo durante una tempesta.

Le dimensioni e la costruzione dello schermo devono essere tali da mantenere la capacità termica il più bassa possibile e consentire un ampio spazio tra gli strumenti e le pareti. Quest'ultima caratteristica esclude ogni possibilità di contatto diretto tra gli elementi di rilevamento del termometro e le pareti, ed è particolarmente importante ai tropici, dove l'insolazione può riscaldare i lati fino a causare un gradiente di temperatura apprezzabile nello schermo. Si deve anche evitare il contatto diretto tra gli elementi di rilevamento e il supporto del termometro.

Lo schermo deve essere dipinto sia all'interno che all'esterno con vernice bianca non igroscopica. Quando sono previste pareti doppie, lo strato d'aria tra di esse serve a ridurre la quantità di calore che altrimenti verrebbe condotta dalla parete esterna verso l'interno, soprattutto in caso di forte irraggiamento solare. Quando il vento è notevole, l'aria tra le pareti viene cambiata continuamente, in modo da ridurre ulteriormente la conduzione di calore verso l'interno dalle pareti esterne. La libera circolazione dell'aria in tutto lo schermo aiuta la temperatura della parete interna ad adattarsi ai cambiamenti dell'aria ambiente. In questo modo, si riduce l'influenza della parete interna sulla temperatura del termometro. Inoltre, la libera circolazione dell'aria all'interno dello schermo consente al termometro di seguire i cambiamenti dell'aria ambiente più rapidamente rispetto a quanto accadrebbe se fossero attivi solo gli scambi radiativi. Tuttavia, l'aria che circola attraverso lo schermo trascorre un tempo limitato a contatto con le pareti esterne e può subire un'alterazione della temperatura. Questo effetto diventa apprezzabile quando il vento è leggero e la temperatura della parete esterna è notevolmente diversa da quella dell'aria. Pertanto, la temperatura dell'aria in uno schermo può essere superiore alla temperatura reale dell'aria in una giornata.

Temperatura dell'aria

Definizione

Il WMO (1992) definisce la temperatura come una grandezza fisica che caratterizza il moto medio casuale delle molecole in un corpo fisico. La temperatura è caratterizzata dal comportamento per cui due corpi in contatto termico tendono a una temperatura uguale. La temperatura rappresenta quindi lo stato termodinamico di un corpo e il suo valore è determinato dalla direzione del flusso netto di calore tra due corpi. La WMO definisce la temperatura dell'aria come "la temperatura indicata da un termometro esposto all'aria in un luogo riparato dalla radiazione solare diretta".

• Unità di misura e scala: Kelvin

• Intervallo: 233,15 K / 323,15 K

• Risoluzione: 0.1 K

• Incertezza: 0,5 K

• Costante di tempo: 20s

• Campionamento: 1Hz

• Tempo di mediazione dell'osservazione in uscita: 60s

Collocazione degli strumenti

I sensori di temperatura vengono racchiusi entro involucri che proteggono dalla radiazione diretta, generalmente ventilati anche in modo artificiale dalle cui prestazione dipende in gran parte il rendimento dei sensori stessi. L'altezza del sensore dal terreno deve essere compresa tra 180 cm e 200 cm.

Umidità dell'aria

Definizione

Le definizioni semplici delle grandezze più frequentemente utilizzate nella misurazione dell'umidità sono le seguenti:

• Temperatura del punto di rugiada Td: la temperatura alla quale, a pressione costante, l'aria (o, più precisamente, la miscela aria-vapore) diventa satura di vapore acqueo.

• Umidità relativa U: il rapporto in percentuale tra la tensione di vapore osservata e la tensione di vapore di saturazione alla stessa temperatura e pressione;

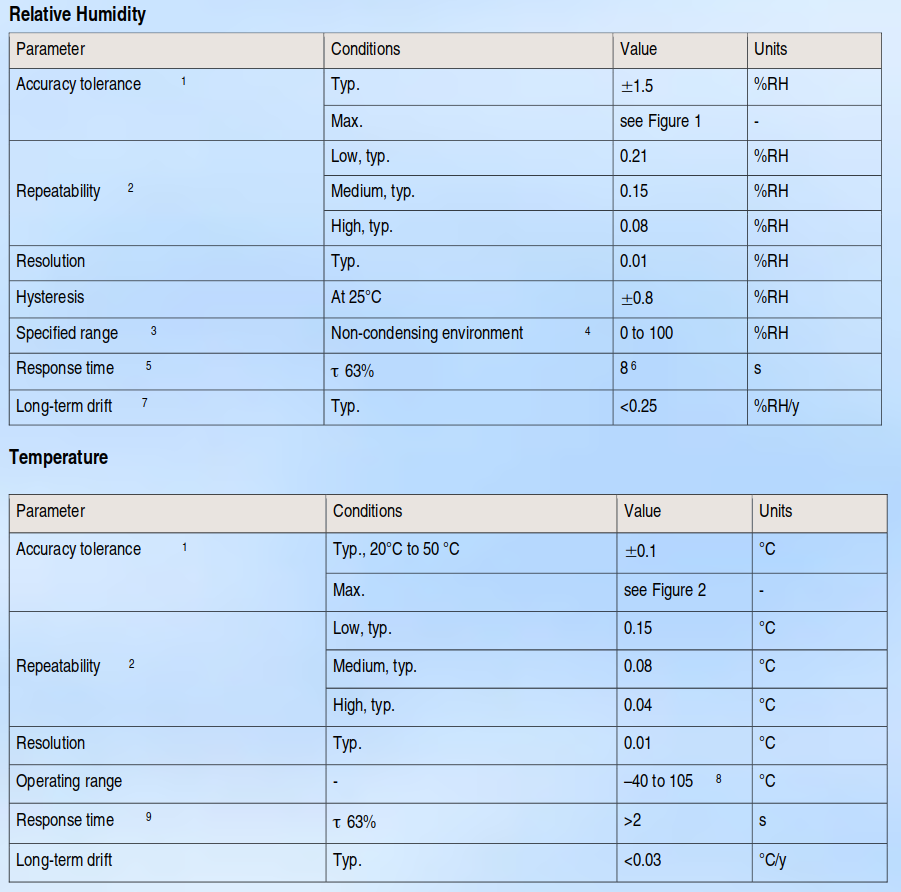
Specifiche

Unità di misura e scala

Temperatura del punto di rugiada	Kelvin
Umidità relativa	percento %

Campo di misura

Temperatura del punto di rugiada	233.15 K / 303.15 K
Umidità relativa	0 - 100

Risoluzione

Temperatura del punto di rugiada	0.1 K
Umidità relativa	2%

Incertezza

Temperatura del punto di rugiada	0.5 K
Umidità relativa	5%

Costante di tempo

Temperatura del punto di rugiada	20 s
Umidità relativa	40 s

Frequenza campionamento

10 Hz

Periodo di media per l'osservazione

60 s

Collocazione degli strumenti

I sensori di umidità vengono racchiusi entro involucri che proteggono dalla radiazione diretta, generalmente ventilati anche in modo artificiale dalle cui prestazione dipende in gran parte il rendimento dei sensori stessi. L'altezza del sensore dal terreno deve essere compresa tra 180 cm e 200 cm.

Strumenti per misurare temperatura e umidità

Strumenti per misurare la temperatura

Come funzionano i sensori digitali

I transistor CMOS hanno la deprecabile caratteristica di variare il guadagno di corrente in base alla temperatura in cui si trovano ad operare secondo una curva caratteristica (della specifica configurazione di sensori) che può essere misurata, a parità di corrente in ingresso per stabilire la temperatura dell’ambiente in cui il sensore opera.

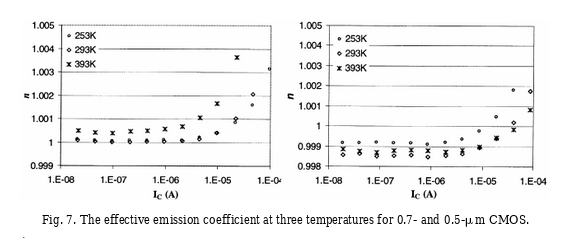
Strumenti per misurare l'umidità

Come funzionano i sensori capacitivi

L'elemento del sensore è costituito da un condensatore. Il dielettrico è un polimero che assorbe o rilascia acqua in modo proporzionale all'umidità relativa dell'ambiente, modificando così la capacità del condensatore. Questa variazione di capacità può essere misurata da un circuito elettronico. In questo modo è possibile determinare l'umidità relativa dell'aria.

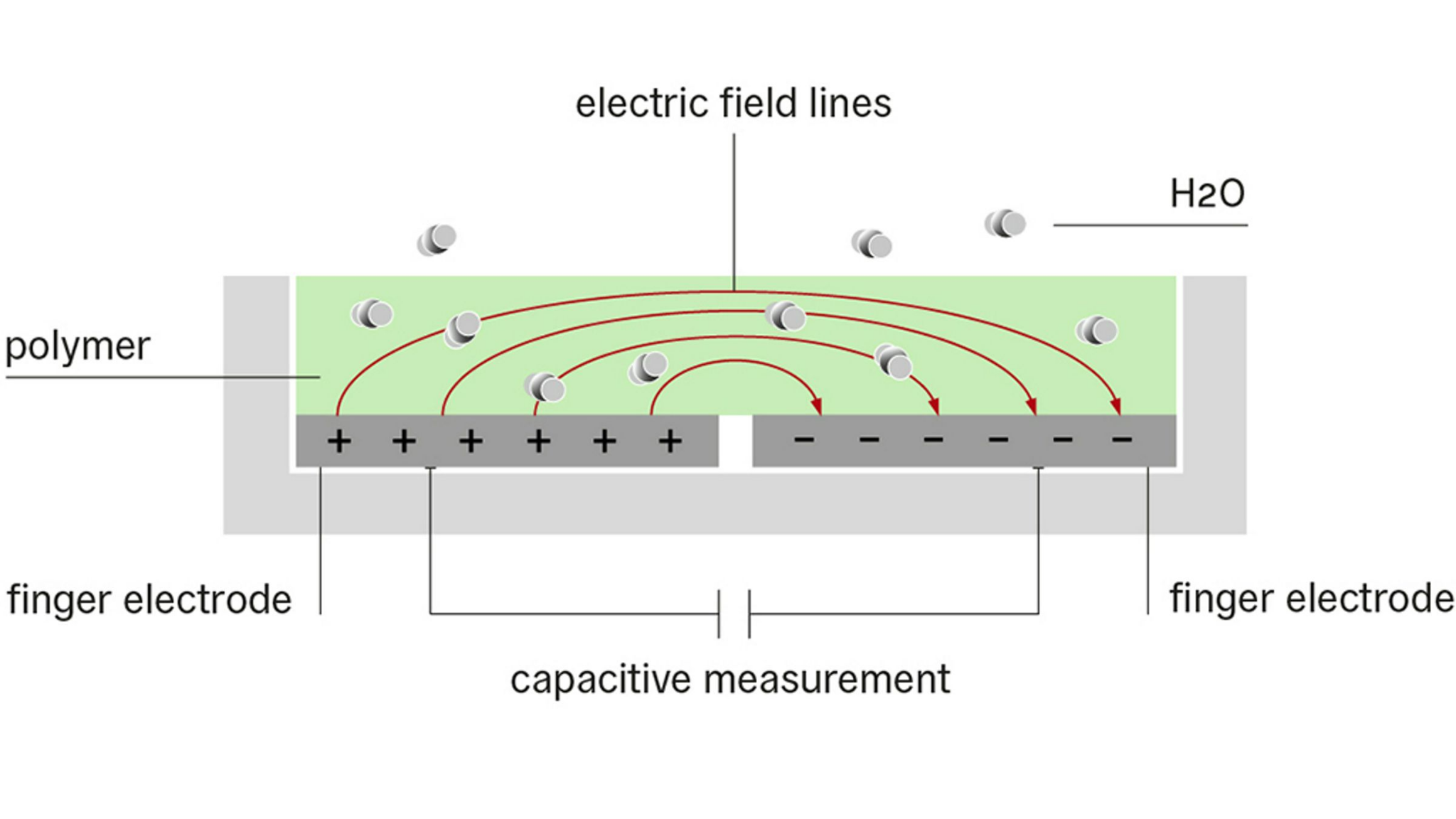
Sensirion SHT85 sensore temperatura e umidità

Uscita digitale completamente calibrata, linearizzata e compensata in temperatura.

L'SHT85 è dotato di una membrana in PTFE dedicata a proteggere l'apertura del sensore da liquidi, sabbia e polvere, secondo lo standard IP67, senza influire sul tempo di risposta del segnale RH.

Humidity Sensors with CMOSens®

Grazie all'esclusivo collegamento di questi elementi del sensore con l'unità di amplificazione del segnale, il convertitore analogico-digitale, la memoria dei dati di calibrazione e l'interfaccia digitale predisposta per il bus, sono tutti posizionati su una superficie di pochi millimetri quadrati.

La conversione analogico-digitale, anch'essa eseguita "in loco", rende il segnale estremamente insensibile al rumore. Per una maggiore affidabilità, viene utilizzato un checksum generato dal chip stesso. Infine, i dati di calibrazione caricati sul chip del sensore garantiscono che i sensori di umidità Sensirion abbiano specifiche identiche e possano quindi essere sostituiti al 100%.

Interfaccia digitale: i sensori di umidità e temperatura con tecnologia CMOSens® possono essere collegati direttamente a qualsiasi sistema a microprocessore tramite l'interfaccia digitale a 2 fili, che riduce al minimo i tempi di sviluppo del sistema, fa risparmiare sui costi e porta a un vantaggio significativo, soprattutto per le applicazioni ad alto volume.

Osservazioni manuali

All'interno del progetto RMAP vengono archiviate misure manuali delle seguenti grandezze:

• altezza del manto nevoso (total snow depth)

• visibilità (visibility)

• tempo presente (current weather)

nel seguito viene data una descrizione della metodologia da seguire per produrre misure corrette di tali grandezze.

Altezza del manto nevoso (total snow depth)

Quando fare la misura

L'altezza totale del manto nevoso va fatta in due casi:

• In presenza di manto nevoso (che verrà misurato in cm)

• Quando è stata prevista una nevicata in un intorno del punto di osservazione, ma nel punto di osservazione non è presente manto nevoso (misura pari a 0 cm)

La misurazione di altezza nulla del manto è stata introdotta recentemente nei disciplinari WMO per distinguere il dato mancante dall'assenza di manto nevoso. In precedenza infatti il dato mancante veniva considerato automaticamente come indicativo di assenza del manto, introducendo un elemento di ambiguità che in alcuni casi ha portato ad errori di valutazione dell'estensione del manto nevoso. Questo errore in alcuni casi si è propagato su tutti i prodotti osservativi a valle fino ad alterare le analisi globali di ECMWF.

Collocazione del sito di misura

Il sito di misura deve consistere di una superficie piana regolare non soggetta ad accumuli anomali rispetto all'area circostante. Il sito quindi deve essere sufficientemente lontano da alberi, edifici, zone di passaggio. In particolare la distanza da ostacoli rilevanti, come edifici o alberi, dovrebbe essere pari al doppio dell'altezza degli ostacoli stessi.

In genere viene consigliata la collocazione sul sito di misura di una tavoletta di legno o compensato levigata e di colore bianco, di circa mezzo metro di lato, simile a quella nella seguente figura e detta Tavoletta Nivometrica. La tavoletta deve essere posta al livello del terreno.

In assenza di tale strumento, la misura si può fare su una qualsiasi superficie piana, possibilmente non metallica e non di colore scuro. Si sconsiglia la misura su un prato, dal momento che la presenza di erba sotto la neve può alterare la misura della altezza totale del manto nevoso.

In generale nel caso non si usi la tavoletta, si consiglia di fare più misure del manto nevoso in più punti nel raggio di qualche metro e di ottenere così il valore della misura finale come media dei campionamenti.

Strumenti di misura

La misura del manto nevoso va fatta utilizzando un righello rigido di lunghezza sufficiente o, meglio ancora, un metro ripiegabile di legno o di plastica, tipicamente utilizzato nei cantieri o dai falegnami, simile a quello in figura.

Come fare la misura

Quando si fa la misura bisogna seguire le seguenti procedure:

• fare attenzione che il righello sia sempre in posizione perpendicolare al piano di misura

• rilevare la misura ponendo sempre gli occhi più vicini possibili al punto di misura, così da evitare errori di parallasse (vedi figura nel seguito).

Visibilità

La misura di visibilità va fatta possibilmente individuando una serie di oggetti o ostacoli (case gruppi di alberi, cartelli stradali, ecc...) a distanza nota dall'osservatore. L'osservazione va semper fatta all'aperto, mai attraverso i vetri di una finestra o di una vetrina e senza usare di strumenti ottici (binocoli, telescopi, o simili). L'osservatore dovrebbe essere posto ad una altezza normale dal suolo (1.5 m circa) e non in cima a torri o balconi. La visibilità dovrebbe essere rilevata in diverse direzioni. Il valore più basso tra queli rilevati rappresenta la misura finale di visibilità.

Tempo presente

Quando si seleziona il tipo di "Tempo presente" bisogna procedere alla selezione di una voce tra quelle riportate nell'elenco. L'elenco è ordinato in base all'intensità e quindi alla rilevanza del fenomeno osservato: fenomeni più intensi o più rilevanti sono più in basso nell'elenco. Man mano ci si sposta in alto nell'elenco, si trovano eventi meno rilevanti. L'osservatore dovrà selezionare l'evento osservato partendo dal basso e potrà inserirne uno solo. Utilizzando questa procedura, inserirà automaticamente l'evento più significativo.

Tabella tempo presente

Codice	Descrizione
100	Nessun fenomeno significativo osservato
101	Nubi generalmente in dissolvimento o con sviluppo in riduzione durante l'ultima ora
102	Stato del cielo generalmente invariato durante l'ultima ora
103	Nubi generalmente in formazione o sviluppo durante l'ultima ora
112	Fulmini in lontananza
110	Foschia (1000m < visibilita' < 10Km)
127	Neve o sabbia sollevata o trasportata dal vento
130	Nebbia (visibilita' < 1000m)
150	Pioviggine (non congelantesi)
155	Pioviggine congelantesi al suolo (moderata)
160	Pioggia (non congelantesi)
165	Pioggia congelantesi al suolo (moderata)
167	Pioggia (o pioviggine) mista a neve, debole
168	Pioggia (o pioviggine) mista a neve, moderata o intensa
171	Neve, debole
172	Neve, moderata
173	Neve, forte
174	Palline di ghiaccio, debole
175	Palline di ghiaccio, moderata
176	Palline di ghiaccio, forte
177	Granelli di neve
178	Cristalli di ghiaccio
184	Rovesci di pioggia o pioggia intermittente,violenta
185	Rovesci di neve o neve intermittente, debole
186	Rovesci di neve o neve intermittente, moderata
187	Rovesci di neve o neve intermittente, forte
191	Temporale, debole o moderato, senza precipitazione
192	Temporale, debole o moderato, con rovesci di pioggia e/o neve
193	Temporale, debole o moderato, con grandine
194	Temporale, forte, senza precipitazione
195	Temporale, forte, con rovesci di pioggia e/o neve
196	Temporale, forte, con grandine
199	Tromba d'aria (Tornado)

Misurare l'isola di calore urbana

Strumenti e metodi di misura L’isola di calore può essere misurata a diversi livelli e con diversa strumentazione:

• S-UHI: in superficie (temperature delle superfici: strade, parchi, tetti) tramite misure in telerilevamento (da satellite)

• C-UHI: nella canopea urbana, in genere con misure “in situ“ da stazioni fisse tradizionali (termometri) Da: Terrascope, EUMETSAT SenJnel 2 + 3

• B-UHI: nell’Urban Boundary Layer (al di sopra della canopea) tramite misure su apposite torri o con sondaggi atmosferici

L'incertezza di misura comprende numerose fonti di incertezza, ciascuna delle quali è detta “componente dell'incertezza” (u 1 , u 2 , … u n ). In particolare, incertezze dovute a:

• calibrazione (di fabbrica, in genere certificata) e taratura (periodica, a carico dell’utente)

• ubicazione della stazione (“sitting“): dipende dal “misurando“ e dalle difficoltà logistiche dell’ubicazione

• esposizione del sensore (“exposure“): dipende dalle difficoltà logistiche dell’esposizione

• altre incertezze(invecchiamento dello shelter, deriva strumentale, ecc.)

NB: Le incertezze (se indipendenti) si compongono al quadrato: u^2 = ∑ ui^2

Ubicazione delle stazioni in ambito urbano

• Le misure devono essere rappresentative di un’area urbana omogenea

• E’ condizionata dalla necessità di risolvere spazialmente l’ambito urbano (scala)

• E’ in genere condizionata da esigenze logistiche (alimentazione, accessibilità, amministrazione, ecc.)

Criteri specifici per stazioni urbane in funzione della scala spaziale orizzontale (WMO - Oke, 2004):

• Mesoscala: le dimensioni tipiche della città, che influenza il tempo e il clima in un’area tipicamente di una o più decine di chilometri. Richiede sempre una rete idonea di stazioni per la sua caratterizzazione.

• Scala locale: comprende strutture urbane e topografiche con esclusione di effetti alla microscala, ad esempio interi quartieri o aree con specifiche attività commerciali o industriali, tipicamente da uno a più chilometri e alcune stazioni.

• Microscala: caratterizza ogni singola superficie o elemento urbano come singoli edifici, strade, giardini o parchi. Varia tipicamente da meno di un metro a centinaia di metri. Richiede almeno una stazione per elemento o tipologia di elemento urbano, standardizzando altezza di misura, tipo di superficie, distanza da ostacoli o elementi estranei. Ad esempio una LCZ è tipicamente a microscala.

• L’effetto sul sensore dipende dalle caratteristiche di un’area posizionata sopravento

• In funzione dell’intensità e della direzione di provenienza dei venti dominanti questo fattore determina la rappresentatività della stazione

• Le percentuali in figura danno un’idea dei contributi che influenzano la misura da parte del sensore in presenza di vento

• In condizioni ideali, l’area circostante il sensore dovrebbe essere sufficientemente omogenea per massimizzare la rappresentatività della misura

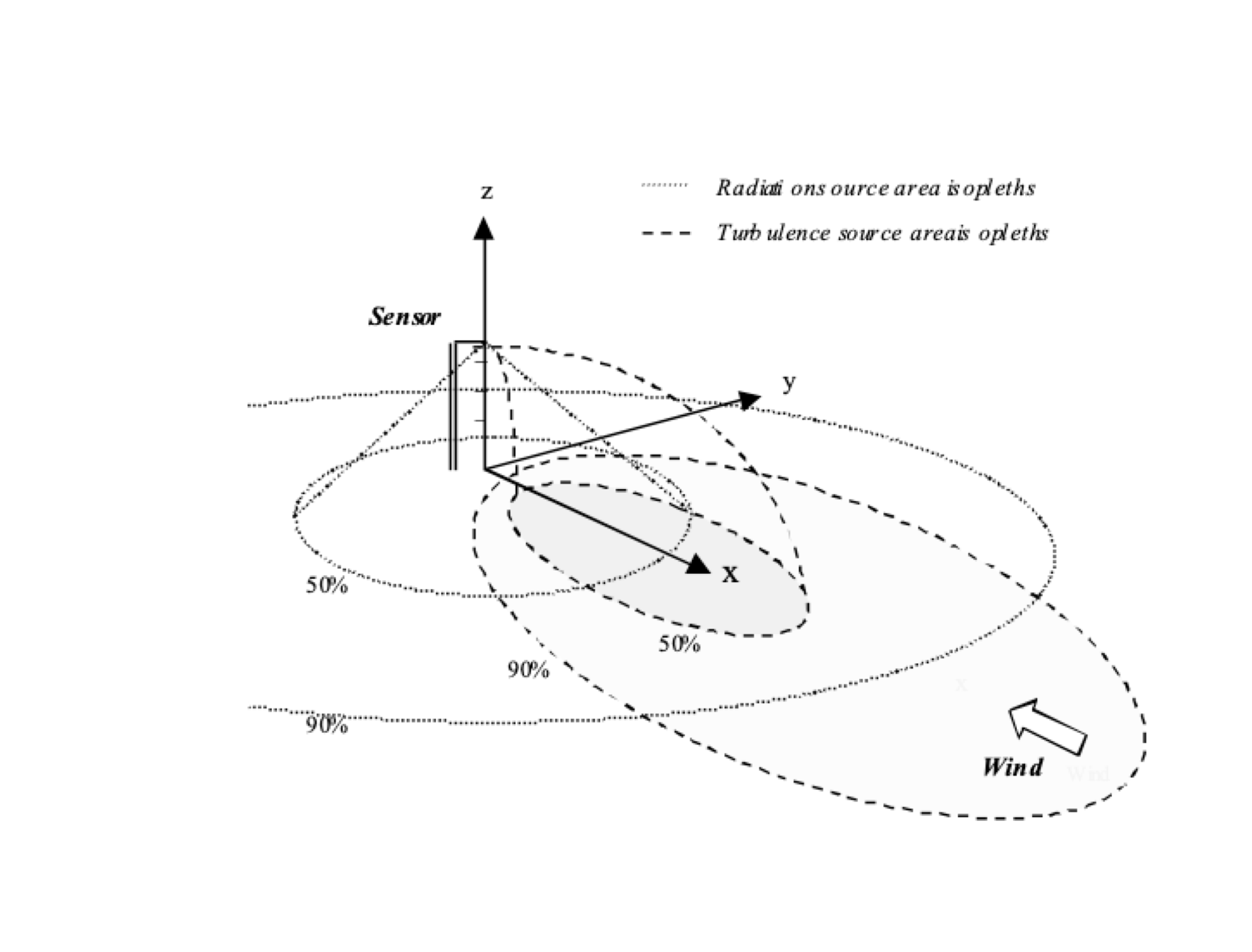
Oke, 2004: –Initial Guidance to Obtain Representative Meteorological Observations at Urban Sites

La scala spaziale verticale:

• Altezza dell’UCL: altezza media degli edifici principali

• Alltezza del RSL: altezza dello strato di rugosità (influenzato dagli edifici)

• U: Profilo verticale del vento medio (spazialmente e verticalmente)

• Zd : Lunghezza di spostamento del piano zero

• Z0 : Lunghezza di rugosità

• ZH : Altezza media degli elementi di rugosità (edifici): definisce l’altezza dell’UCL

• Zr : Altezza dello strato di rugosità: definisce l’altezza del RSL

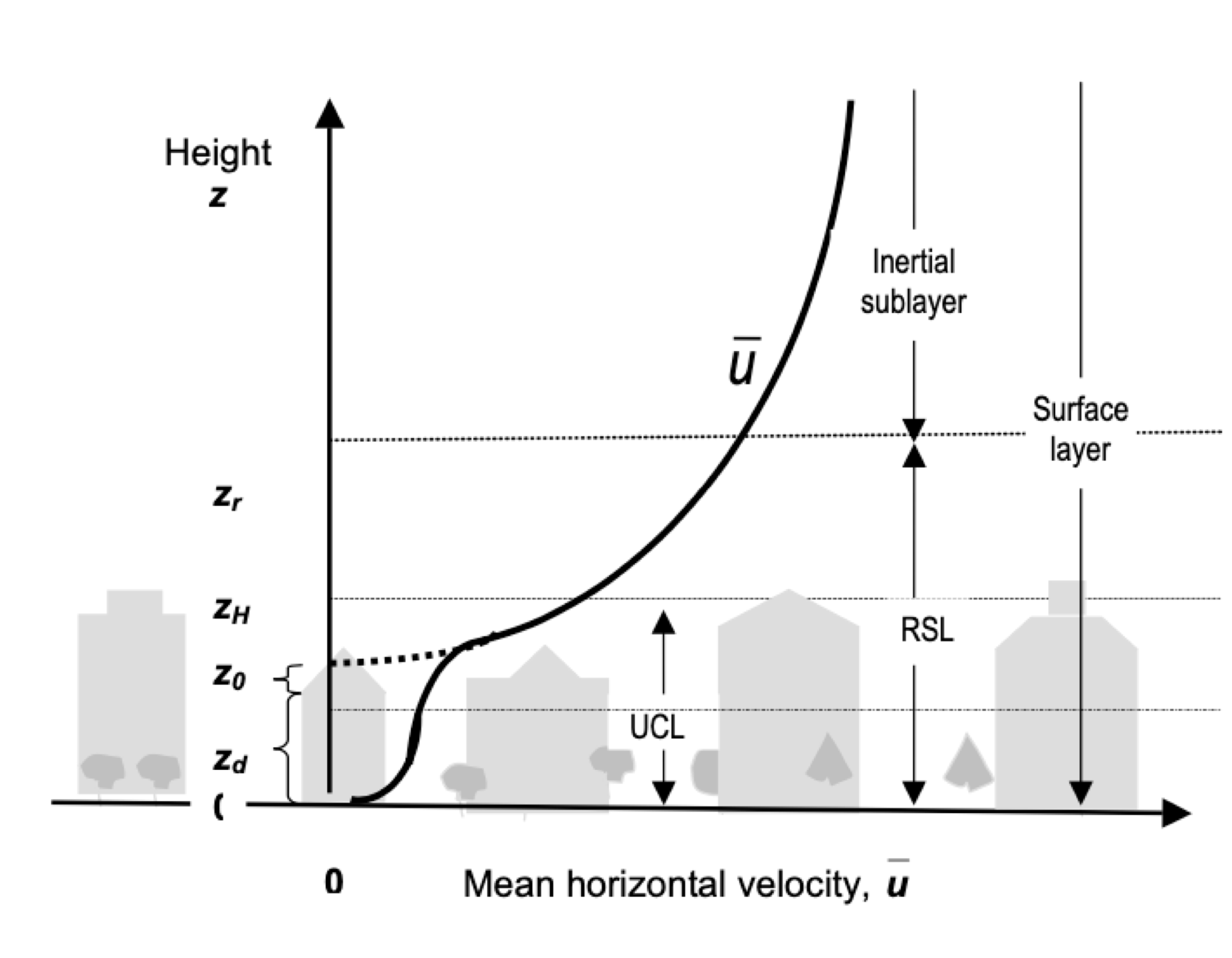
Esposizione dei sensori per le misure in ambito urbano

• Le misure devono essere fatte su superfici che a microscala siano rappresentative dell’ambiente urbano a scala locale

• I sensori devono essere centrati su un’area aperta dove il rapporto altezza/distanza degli edifici sia rappresentativo dell’ambiente circostante

• In una strada, il rapporto altezza/distanza degli edifici si applica alla sezione della strada stessa. L’asse della strada dovrebbe essere in direzione N-S. L’altezza dal suolo è preferibilmente superiore ai 2 metri.

• Particolare attenzione va dedicata all’efficienza della schermatura dalla radiazione di cui si raccomanda la ventilazione forzata

• Posizionare i sensori ad almeno 5 ÷ 10 m da edifici più alti di 20 ÷ 30 m.

• Attenzione ai camini e griglie di ventilazione!

• La temperatura misurata sopra l’UCL (sensori su un palo), è influenzata non solo dall’aria scambiata con l'UCL ma anche dai tetti.

• I tetti sono in genere molto più variabili termicamente di tutte le altre superfici.

• All’interno dell’UCL la temperatura cambia relativamente poco con l’altezza, ma c’è in genere una discontinuità al livello dei tetti sia verticalmente che orizzontalmente: è pertanto preferibile posizionare i sensori ben al di sopra dei tetti circostanti.

• L’estrapolazione di una misura sia in senso verticale che orizzontale è molto problematica (i metodi statistici possono funzionare, ma richiedono lunghe serie in genere non disponibili)

Misure Qualità dell'aria

Classificazione delle stazioni di monitoraggio

Non tutte le stazioni di monitoraggio della qualità dell’aria sono uguali. Possono differenziarsi per il tipo di sensori installati, per la loro posizione, e per il tipo di misurazione a cui sono preposte.

L’Agenzia Europea per l’Ambiente (https://www.eea.europa.eu/it) ha stilato dei criteri per la classificazione di questo tipo di centraline a seconda della loro tipologia e delle caratteristiche dell’ambiente in cui sono installate. Senza voler scendere troppo nei dettagli, possiamo dividere le stazioni in tre grandi categorie:

misurazione dell’inquinamento da TRAFFICO (T): stazioni che misurano il livello di inquinamento generato prevalentemente da emissioni da traffico, provenienti da strade limitrofe con intensità di traffico medio alta;

misurazione dell’inquinamento di FONDO (B): stazioni posizione lontano da specifiche fonti di inquinamento (industrie, traffico, riscaldamento residenziale, etc.) che non sono influenzate, cioè, da una fonte prevalente di inquinamento.

monitoraggio di fonti di inquinamento INDUSTRIALI (I): stazioni ubicate in una zona in cui l’inquinamento sia generato in prevalenza da singole industrie o da vicine zone industriali

Anche l’ambiente che accoglie la stazione viene categorizzato dalla stessa direttiva e suddiviso in aree di tipo Urbano (U), Suburbano (S) e Rurale (R).

Le aree urbane sono quelle densamente popolate, quelle suburbane, o periferiche, sono caratterizzate da un'alternanza di aree edificate ed aree libere da edifici, quelle rurali possono essere caratterizzate per esclusione.

Questa classificazione di massima viene affinata in base all’attività umana prevalente in aree Residenziali (R), Commerciali (C), Industriali (I), Agricole (A) e Naturali (N).

Le stazioni vengono indicate con una sigla che ne rappresenta il tipo, ad esempio, ad una stazione di misurazione del traffico situata in un’area urbana a vocazione commerciale sarà attribuito il codice TU-C, ad una che misura l’inquinamento di fondo in periferia, quello BS-R (in caso la prevalenza di strutture antropiche sia di tipo residenziale).

Non tutte le combinazioni di questi fattori possono essere utilizzate, ad esempio non sarà mai possibile classificare una stazione come TU-N perché per definizione un’area urbana, registra una forte presenza umana. A seconda dell’ambiente che le ospita, si considera che le stazioni coprano un’area che va da circa 200m² di una stazione installata in ambito urbano a diverse decine di chilometri per le stazioni situate in un ambiente rurale, o a centinaia di chilometri quadrati nel caso di aree rurali remote (distanti più di 50 km da centri abitati e zone industriali).

Le misurazioni attese dalle stazioni, quindi, dipenderanno dalla loro tipologia. La valutazione delle letture effettuate dovrà tenere conto delle stazioni circostanti e di altri fattori che sarebbe fuori luogo elencare in questo documento ma che possono essere un valido spunto di discussione da approfondire in classe.

Nelle linee guida per la predisposizione delle reti di monitoraggio della qualità dell’aria, l’Istituto Superiore per la Protezione e la Ricerca Ambientale individua le scuole come luoghi adatti all’installazione di stazioni di background urbano e suburbano.

Criteri per la selezione del sito di installazione

Per far sì che i dati raccolti dalle stazioni possano essere paragonabili, è importante che il posizionamento di queste ultime sia il più possibile omogeneo. Due sensori che misurano la concentrazione di particolato, posizionati su un palazzo, e posti uno a piano strada, e l’altro sul lastrico solare, ad esempio, daranno, nello stesso istante, valori che possono essere molto diversi tra di loro.

Le linee guida sono particolarmente dettagliate sul tipo di posizionamento dei punti di misura di una stazione in base ai parametri monitorati ed al tipo di stazione.

Allo stato attuale, le stazioni Stima misurano, oltre a temperatura ed umidità, PM2.5, PM10, CO2. Idealmente una stazione che registra questo tipo di parametri, dovrebbe essere posizionata ad altezza uomo intorno ai 2m dal livello del suolo, ma, per proteggere l’apparato da manomissioni e furti, si può prendere in considerazione la possibilità di posizionarle ad un’altezza che varia tra i 2 e 4 metri.

Visto che le concentrazioni di particolato diminuiscono con l’altezza, sarebbe opportuno che tutte le stazioni fossero installate ad un'altezza simile.

Anche la distanza dall’edificio che dovesse dare loro supporto influenza le misurazioni. Se possibile, bisognerebbe usare una staffa che distanzi la stazione di almeno 20 centimetri dal muro che la sostiene.

È importante assicurarsi che ci sia un buon circolo d'aria attorno alla stazione. In caso contrario i valori registrati potrebbero essere sottostimati. Anche una posizione troppo esposta potrebbe portare a valutazioni inesatte. Ad esempio, la turbolenza prodotta dai veicoli in transito potrebbe portare a misurazioni più alte dei valori realmente.

La stazione Stima ha bisogno di essere alimentata continuamente e di trasmettere periodicamente i campioni perché possano essere trasformati in osservazioni utilizzabili. Per fare ciò è necessario assicurarsi che il punto prescelto permetta alla stazione di collegarsi tramite rete Wi-Fi ad internet. Potrete trovare alcuni criteri per permettere un utilizzo sicuro e protetto della connessione più avanti in questa guida.

Strumenti per misurare il particolato

Come funzionano i sensori di particolato atmosferico a base ottica

I sensori utilizzano le proprietà della diffusione della luce per misurare il conteggio, le dimensioni e la concentrazione delle particelle. I componenti di base sono: sorgente luminosa diretta alle particelle, rivelatore per misurare la luce diffusa dalle particelle e circuiti elettronici che elaborano e analizzano l’uscita del rivelatore.

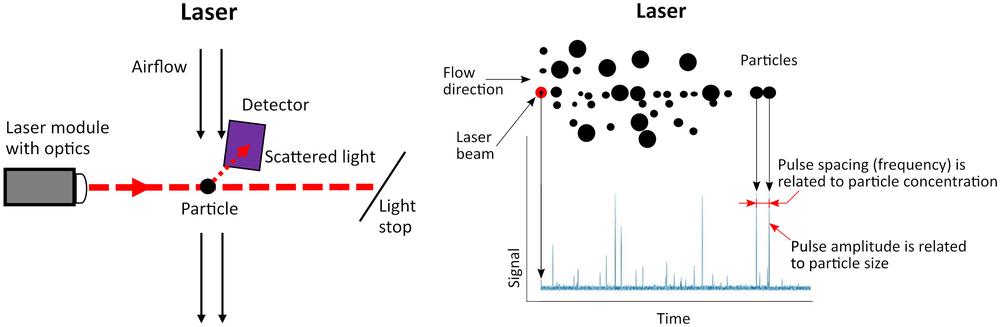
Sensore per particolato Sensirion SPS30

Un laser con lunghezza d’onda adeguata, è intercettato da un flusso d’aria che porta in sospensione le particelle di particolato che intendiamo misurare. Un diodo, in posizione defilata, misura la luce diffusa e calcola una stima delle particelle sospese nel flusso d’aria esaminato.

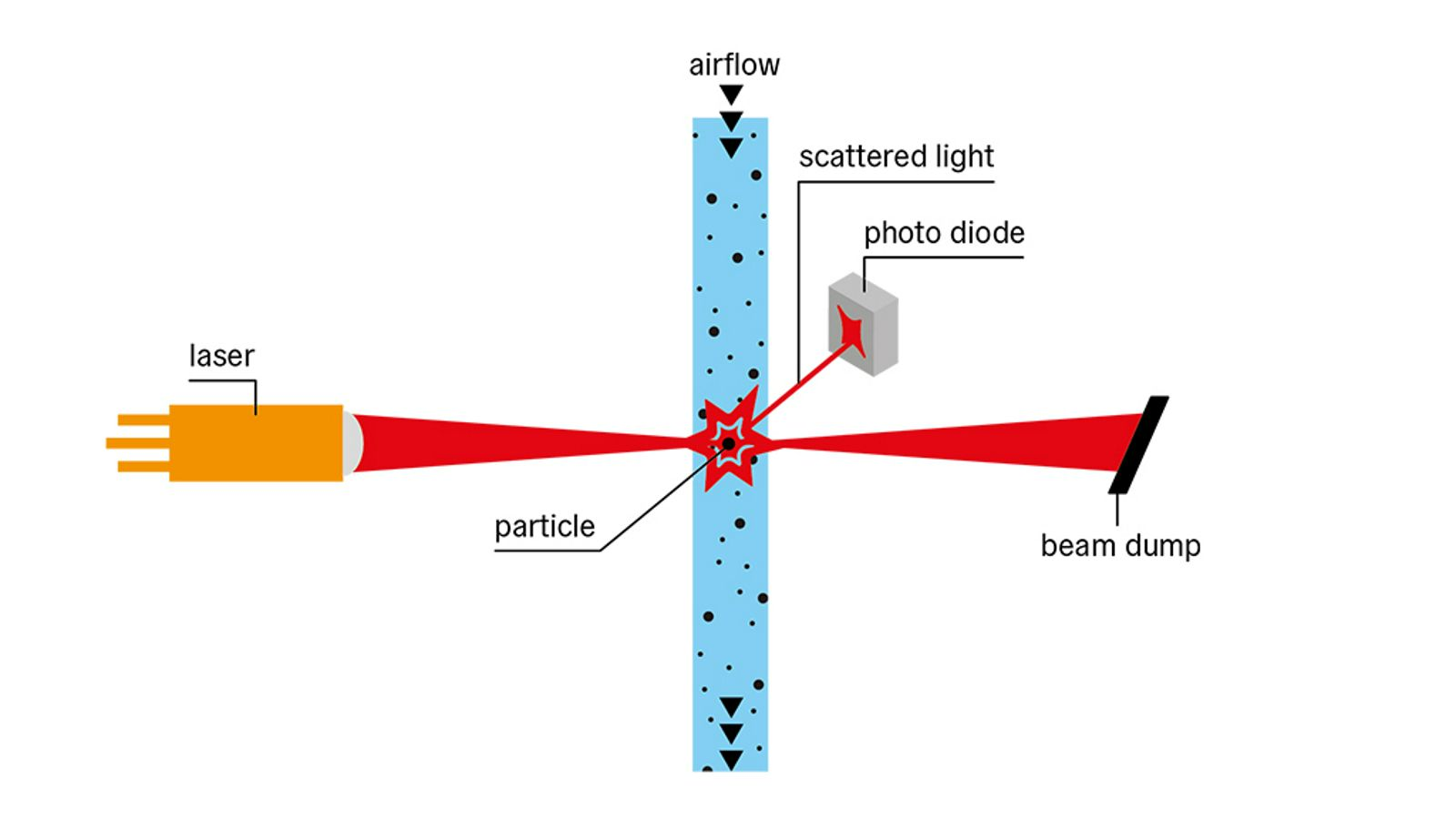
Il problema più grosso, a parte capire la natura ondulatoria della luce, consiste nel mantenere puliti emettitore e ricevitore che si troverebbero costantemente immersi in un ambiente ostile (e bisognosi di manutenzione e pulizia). Un flusso lamellare (semplifichiamo) di aria pulita filtrata impedisce al particolato di depositarsi e ridurre la precisione del sensore nel tempo.

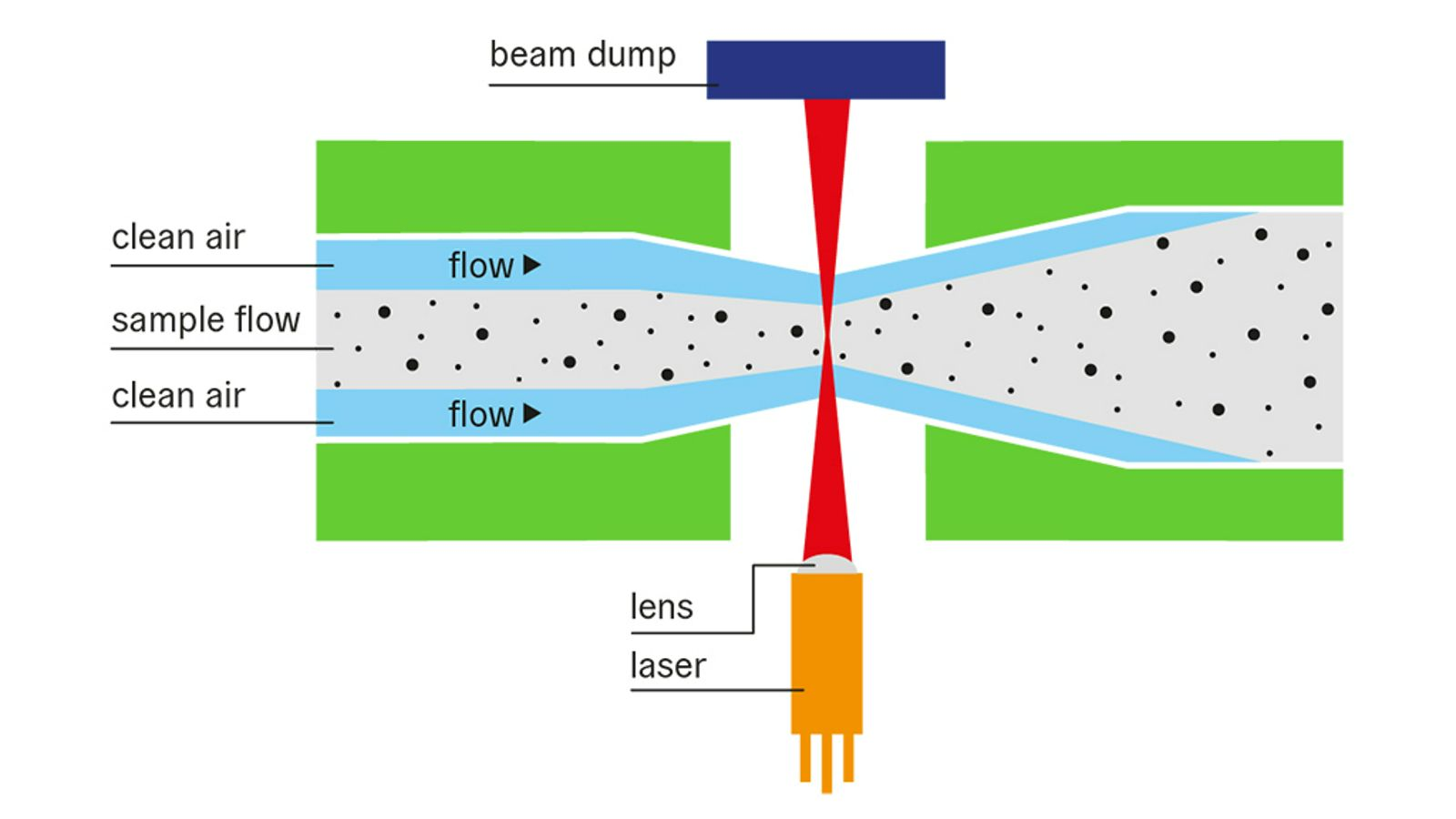
• Sensore completamente calibrato con interfaccia UART e I2C

• Classificazione avanzata delle particelle per dimensione (binning delle particelle):

• Concentrazione di massa: PM1.0, PM2.5, PM4 e PM10;

• Concentrazione numerica: PM0.5, PM1.0, PM2.5, PM4 e PM10.

• Dimensioni di 40,6 x 40,6 x 12,2 mm

• Limite inferiore di rilevamento è di soli 0,3um

• Durata superiore a otto anni pur funzionando ininterrottamente per 24 ore al giorno senza necessità di pulizia e/o manutenzione

• Il raggio laser è focalizzato su una piccola area

• Diametro del punto luminoso ridotto => alta densità di potenza

• La particella diffonde una grande quantità di luce => rapporto S/N grande

• Le particelle restituiscono segnali individuali

• Le particelle troppo grandi possono essere escluse dalla lettura di massa

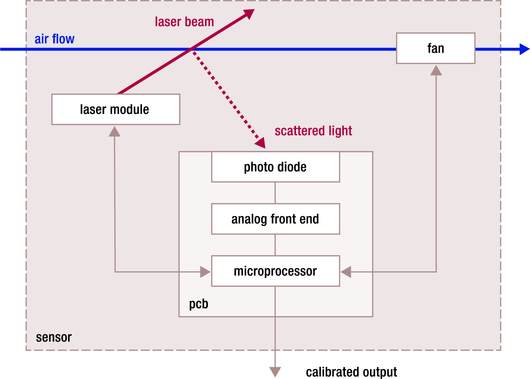
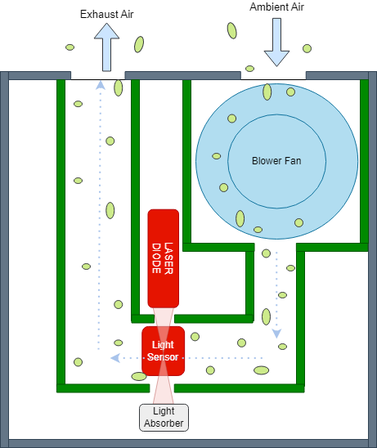
Principio di funzionamento

Un flusso d'aria controllato viene creato all'interno del sensore per mezzo di una ventola. Un circuito di feedback interno tra il microprocessore e la ventola stabilizza la velocità della ventola e quindi il flusso d'aria attraverso il sensore.

Il PM ambientale viaggia all'interno del sensore dall'ingresso all'uscita, trasportato dal flusso d'aria.

In corrispondenza del fotodiodo, le particelle presenti nel flusso d'aria attraversano un raggio laser focalizzato che provoca la diffusione della luce.

La luce diffusa viene rilevata dal fotodiodo e convertita in una concentrazione di massa/numero attraverso gli algoritmi proprietari di Sensirion, eseguiti dal microcontrollore interno a SPS30.

Strumenti per misurare la CO2

Come funzionano i sensori NDIR

Il sensore NDIR (Non Dispersive Infra-Red) sfrutta il fatto che le molecole di CO2 assorbono la radiazione infrarossa di determinate lunghezze d'onda. Maggiore è la concentrazione di CO2, maggiore è la quantità di radiazioni assorbite dalla CO2. La lunghezza d'onda di 4,3μm presenta il massimo assorbimento per la CO2 e un assorbimento minimo per gli altri gas presenti nell'aria.

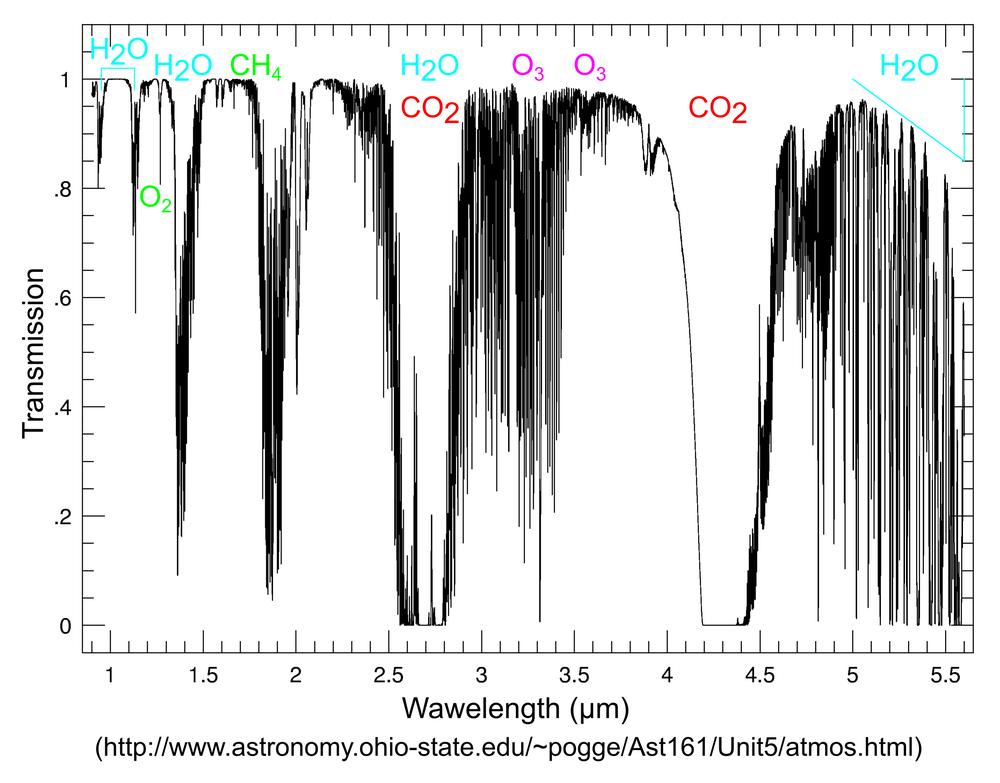
La sorgente di radiazione infrarossa (lampadina) è posta su un lato del tubo. Sul lato opposto sono collocati due sensori con filtri ottici. Il primo sensore (CO2) ha un filtro passa-banda per la lunghezza d'onda di 4,3 µm; misura l'intensità della radiazione Id. Il secondo sensore (riferimento) ha un filtro passa-banda per la lunghezza d'onda solo minimamente assorbita dai gas presenti nell'aria (tipicamente 4µm); misura l'intensità della radiazione I0.

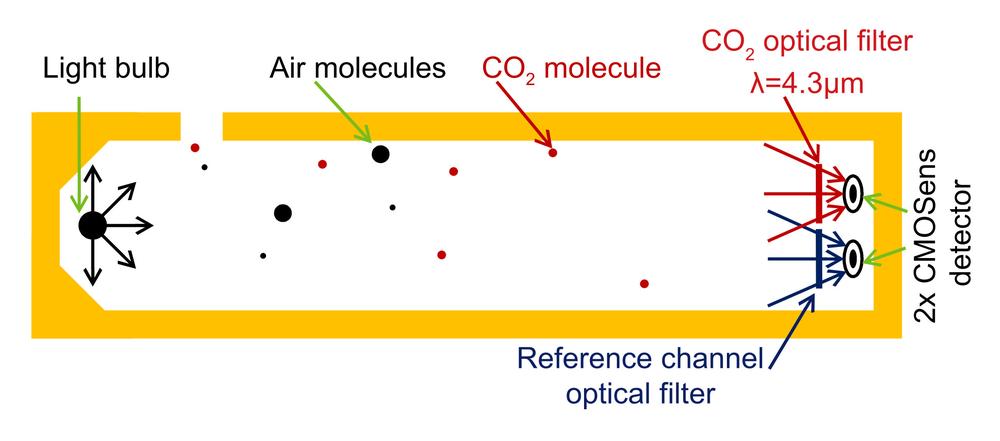
L'intensità misurata della radiazione a queste lunghezze d'onda è quindi associata alla concentrazione di CO2 tramite la legge di Beer-Lambert, data dalla seguente equazione:

Id/I0=e^KCL

• Id è l'intensità della radiazione a 4,3μm,

• I0 è l'intensità della radiazione di riferimento

• K è il coefficiente di assorbimento della CO2

• C è la concentrazione di CO2

• L è la lunghezza del percorso tra la sorgente di radiazione e i rilevatori di luce

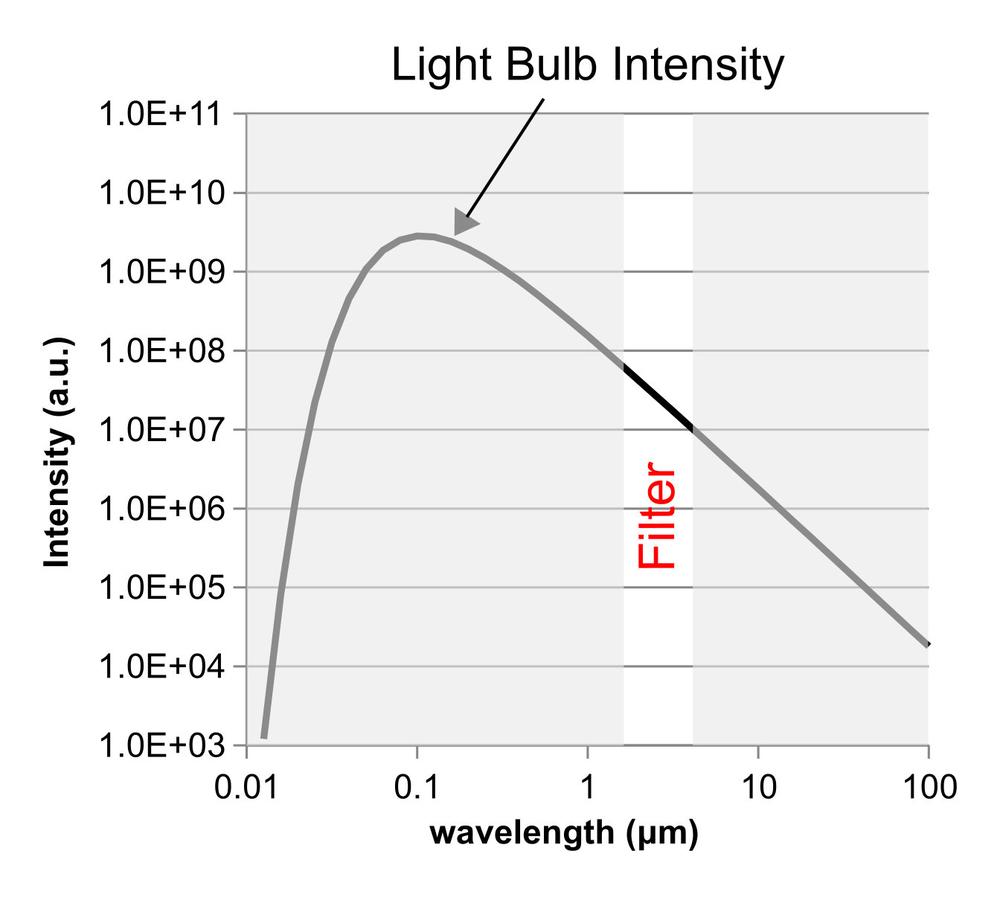
Il sensore di riferimento compensa l'effetto della variazione dell'intensità della radiazione. Quando l'intensità varia, sia Id che I0 cambiano in modo identico, quindi Id / I0 rimane invariato.

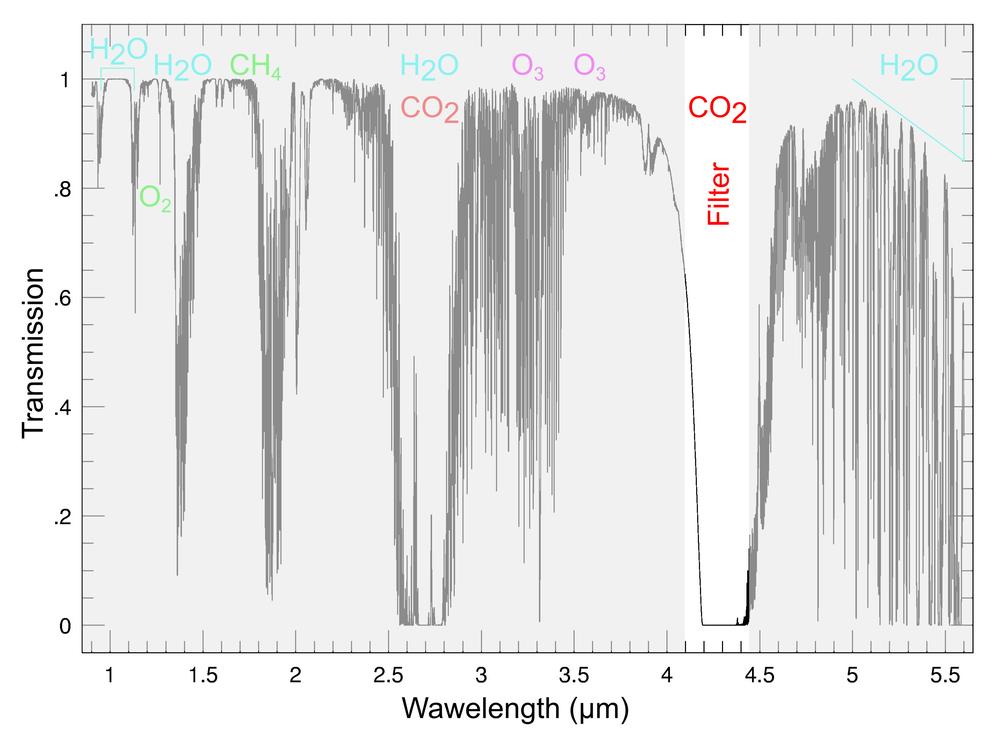
Sesirion SCD30 NDIR CO2 Sensor

Il sensore di CO2 funziona sfruttando la tecnologia NDIR. Un laser infrarosso emette una radiazione con una lunghezza d’onda di 4.26-micron (che è nella banda di assorbimento della CO2) in un ambiente di test. Un ricevitore, dalla parte opposta della camera di acquisizione misura gli infrarossi non assorbiti durante il tragitto per effettuare la misura. È il sistema più usato per misurare la CO2

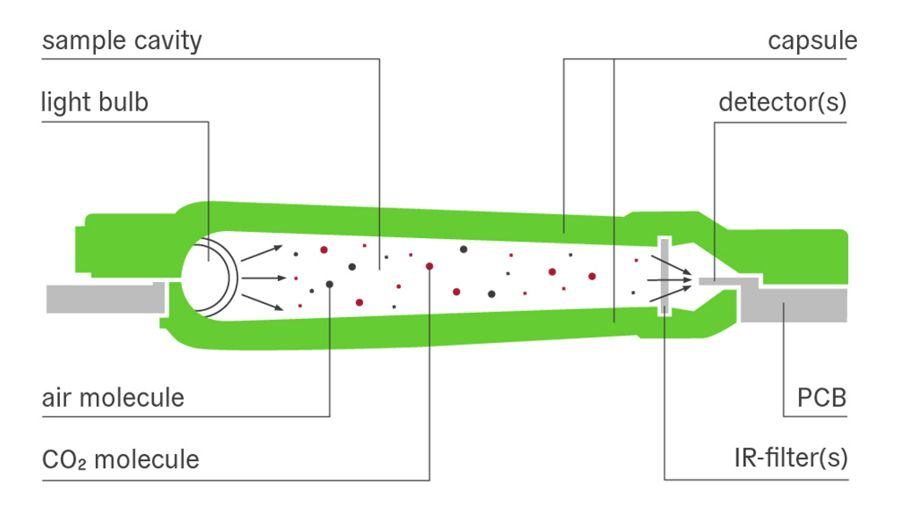
• CO2 measurement range 0 – 10’000 ppm

• Accuracy ± 30 ppm ± 3% (25 °C, 400 – 10’000 ppm)

• Repeatability 10 ppm

• Temperature stability 2.5 ppm / °C (0 – 50 °C)

• Response time (t63): 25 s

Sensirion SCD40 Sensore CO2 (Photo Acoustic Sensor)

Una tecnologia alternativa proposta da Sensirion, che permette sensori più compatti e, a detta loro, più precisi. Usa sempre una fonte a infrarossi con lunghezza d’onda di 4.26-micron (riga caratteristica della CO2) ma fa leva su un principio diverso. Le molecole di gas eccitate dalla fonte luminosa, vibrano e influenzano la pressione all’interno di una struttura rigida. Variazione di pressione che può essere valutata usando un microfono. Tecnica proprietaria senza ulteriori indicazioni (ad ora)